作者：孙宇熙，张建松，王昊

我们知道关系型数据库使用SQL语言和二维表结构来描述世界，这与图数据库所用的方式形成了鲜明的对比——由于现实世界和图都是高维的，图数据库被认为是可以天然的100%还原世界。然而图的这种天然性必然给我们带来一些挑战——特别是对于那些习惯于零和博弈理论的人来说——它需要人们开动脑筋放手一搏，跳出固有框架和限制性思维，意识到SQL、RDBMS并非建模之王道。

在前面的一篇关于数据库查询语言演变的文章中，我们描述了SQL和NoSQL的演变及优缺点。在时下的商业环境中，越来越多的企业依靠图分析和图计算来增强其商业决策能力。

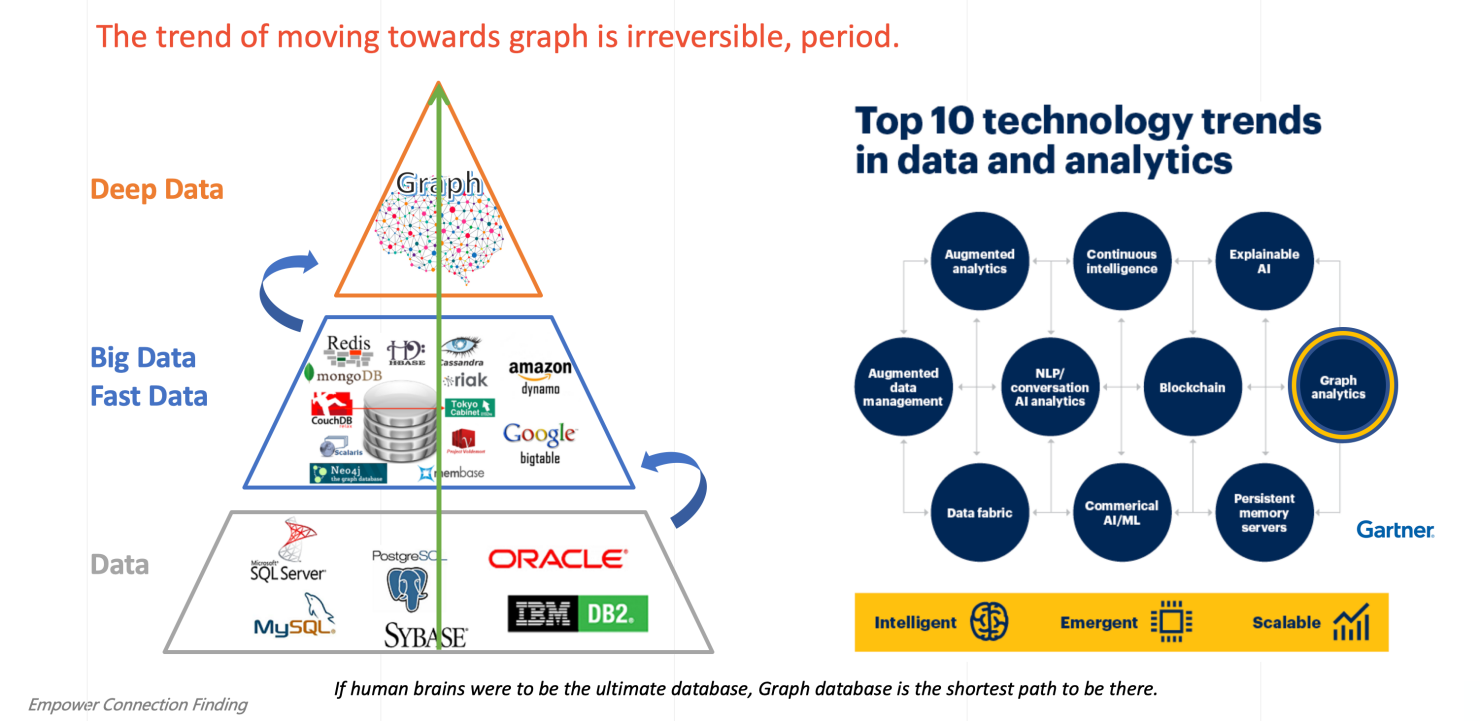
深数据和图分析的主要趋势 --- 202x

Gartner在其2019年底至2021年中发表的一系列趋势分析中将图分析列为十大数据和分析趋势之一（见上图），并表示到 2025 年全球 80% 的商业决策创新都将基于图分析做出。

现在思考这样一个问题：图数据库应该具备什么样的顶级功能——这个问题的答案直指SQL和RDBMS所缺少的功能。

像这种开放式问题，答案通常是丰富多样、没有标准的。然而，在所有可能的答案中，有三件事一定会引起您的共鸣，它们是：

• 简单性（回想一下编写上百行SQL的痛苦）
• 递归操作（递归查询）
• 速度（实时性）

接下来我们就倒序讲解以上三个概念。

速度

提供像闪电般快速的查询本就是图数据库设计的初衷。传统的表关联在大量产出数据时的速度奇慢无比，因此从根本上改变数据的构建方式是至关重要的。站在高维的角度观察可以发现，图将人类世界中的实体连接成网络（树状或图状）之后，对实体的探索工作就可以转化为在图中寻找顶点的邻居、查找顶点和顶点之间的路径、查找任何一对顶点之间共享的公共属性（相似性），计算图或子图的中心性、计算顶点在图中的排名等。像这样对图进行处理并从中挖掘信息的方法还有很多。尽管大多数人倾向于接受“图越大、越密、查询越复杂，必定使相关的图计算性能更低下”，但事实并非如此

考虑以下场景：在一个由数百万用户组成的社交网络图中，查找 200 对用户（年龄分别为 22 岁和 33 岁），要求他们之间有不超过 9 个中间用户，并测量性能下降（如有）的情况。

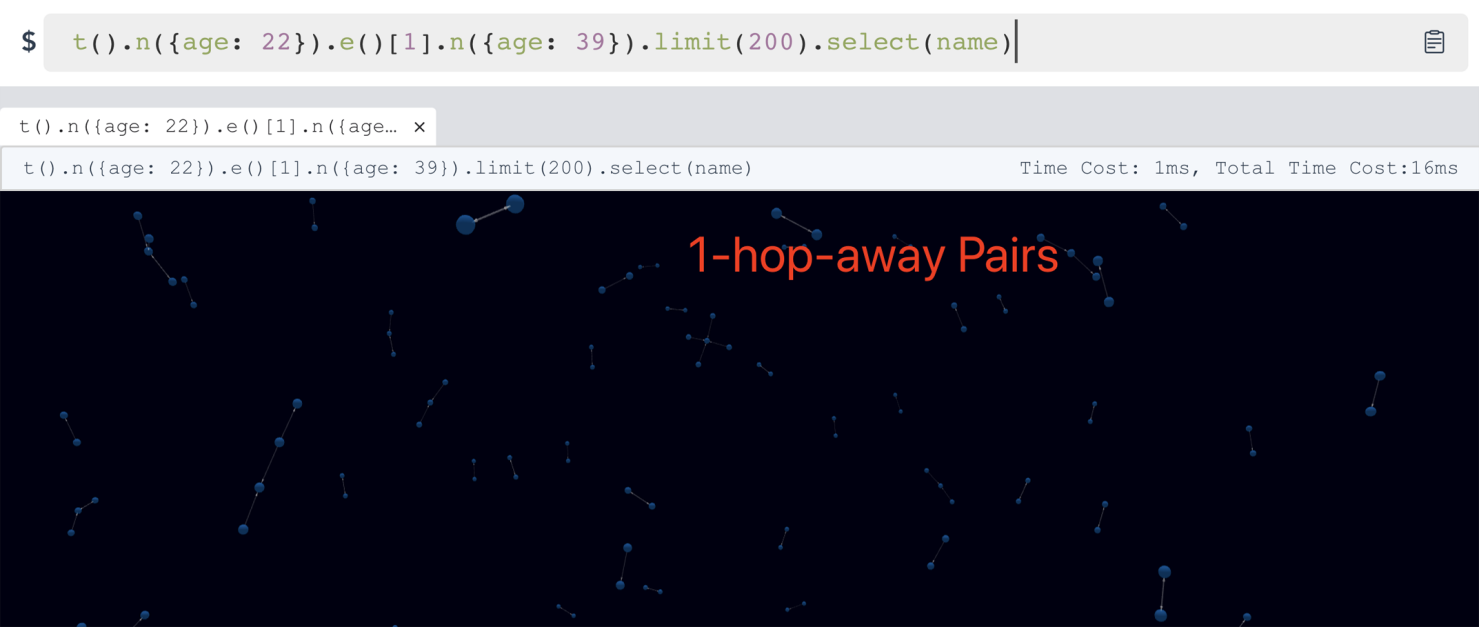
嬴图数据库实时深图遍历

上面的截图显示了嬴图数据库对 Amazon-0601 图数据集（350 万条边和 50 万个顶点，具有id、名称、年龄、关系类型、等级等多个属性）上执行上述查询所需的时间，所使用的是基于模板路径的查询条件，从1-hop开始，逐渐深入到10-hop。下图捕获了执行时间（延迟）的比较：

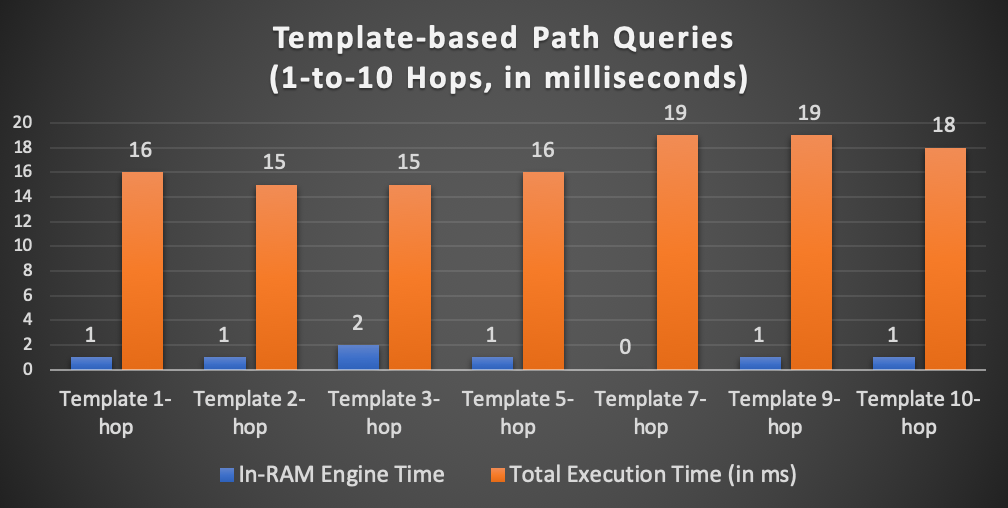
嬴图 - 图遍历延迟对比

正如您所看到的，当我们深入遍历到图中时，整体延迟增长趋势平稳（总时间为1-hop/16ms到10-hop/18ms，内存计算时间则为1-2ms或更低），并没有明显的性能下降。此外，IN-RAM计算引擎极大地加快了处理速度，其延迟占总延迟的 5% 到 10%——绝对成本非常之低。

不同于传统的无状态、分散的网页应用程序，图是具有整体性的。与整体性相反的，如果整个图被分发到不同的集群实例中，由于这些实例会相互依赖以获得计算所需的中间结果，那么任何需要针对所有实例进行处理的查询都将显著降低总体系统的性能——这是任何 BSP（大型同步处理）系统所面临的共同难题。为了避免这个难题，需要尽可能以完整的方式存储图的架构，图的属性等维度的信息则可以分散在不同的集群中！

上面一段内容应该会令读者有所启发，进而明白为什么 JanusGraph、AWS Neptune 或 ArangoDB 等众多商业数据库会缓慢至极——它们的核心弱点在于盲目地使用了复杂的分布式体系结构设计。

暂且撇开分布式策略不谈，加速图查询（如路径查找、K邻查询）最重要的技术是通过高密度计算、深度遍历以及动态剪枝。然而，这些本是最基本的技术却长期被许多程序员所遗忘。诚然，在高级编程语言当道的今天，数百万新一代的年轻程序员们都拥趸 Python 的无所不能和易用性。但就处理能力而言，Python 显然是很有问题的，Java 以及任何专注于 GC 的语言也是如此。

并行架构设计与存储优化（图灵讲座 2018）

在由 ACM 举办的 2018 年度图灵讲座中，图灵奖得主 David Patterson 和 John Hennessy 介绍了在18核Intel X86-64 CPU上使用并行C将串行的Python程序提速 62000倍以上，该成果使用了三种性能优化路径：

• 贴近底层硬件的编程语言
• 内存加速
• CPU高级指令集功能使用

这些技术都有助于实现高密度计算。此外，通过数据结构创新，实现了运行时动态图剪枝和深度图遍历。在《图数据结构的进化》一文中介绍过的邻接哈希结构，可以有效地存储图拓扑结构并启用实时过滤（也称为动态图修剪或剪枝）——当然，最引人注目的是，就时间复杂度而言，图上的大多数操作都是 O(1)，而不是 O(logN) 或 O(N) 甚至 O(N * logN)，也就是说在深入进行图遍历时不会产生指数级增长的搜索复杂度，这一点至关重要。以下是嬴图数据库在 Amazon-0601图数据集上进行的“指数挑战”的结果：

• 边-点比 = 8 (平均来讲就是连接每个顶点的边的数量)
• 1 步路径的搜索复杂度 ~= 8
• 2 步路径的搜索复杂度 ~= 8*8 = 64
• ...
• 5 步路径的搜索复杂度 ~= 8*8*8*8*8 = 32,768
• ...
• 10 步路径的搜索复杂度 ~= 1,073,741,824
• 200 对不同起点/终点的 10 步路径的搜索复杂度 ~= 200,000,000,000

显然，如果复杂度真的超过 2000 亿，任何图系统都无法在毫秒内返回搜索结果。上述复杂度只是理论上的，实际情况要乐观得多。一个 O(1) 级别的操作在真实搜索中其最大可能的搜索复杂度绝不会超过图中的总边数（对于所用的 Amazon 0601 图集来说是 350 万条），因此我们可以假设从第 7 层（32768 * 8 * 8）开始到任何更深的层数，最大复杂度的上限为 350 万条（Amazon 0601 的真实复杂度实际上约为 20 万，特别是 6 到 8 层的深度）：

• 6~10 步路径的调整后的搜索复杂度 <= 200,000 每步

于是可以将图遍历延迟的边界情况记录如下：

O(1) 复杂度与延迟边界值

将此图与先前的“图遍历延迟”中的情况相比较不难得出结论：通过利用最大并发（并行化）和CPU 缓存，嬴图实现了接近底层硬件平台极限的延迟水平。在任何其他图数据库（即Neo4j、TigerGraph、D-graph、ArangoDB，或任何其他成熟与否的产品）上进行相同的操作都将花费比HDD或SSD耗时长得多的时间，或者在进行深度查询时无法返回（TigerGraph可能位于 SSD 和 IN-RAM 之间，但无法返回深度超过10层的遍历操作）。

递归操作

在介绍过速度和性能之后，现在要讨论图数据库的一个独特的应该被普遍使用的特征——递归操作。

让我们再次回顾上一个查询：

Find 200 pairs of users (starting from users whose age=22, ending with users age=33) who are exactly X-hop away from each other. Assuming X=[1-10]

查找 200 对用户（年龄分别为 22 岁和 33 岁），要求他们之间有不超过 9 个中间用户

从设计查询语言的视角进行观看，该如何使用查询语言描述这个问题并获取答案呢？

设计的关键在于让查询具有叙述性，这意味着查询语言要像人类的语言那样易于理解，并具有递归性和简洁性，这样就不必费劲编写晦涩的逻辑了。

t().n({age: 22}).e()[10].n({age: 39}).limit(200).select(name)

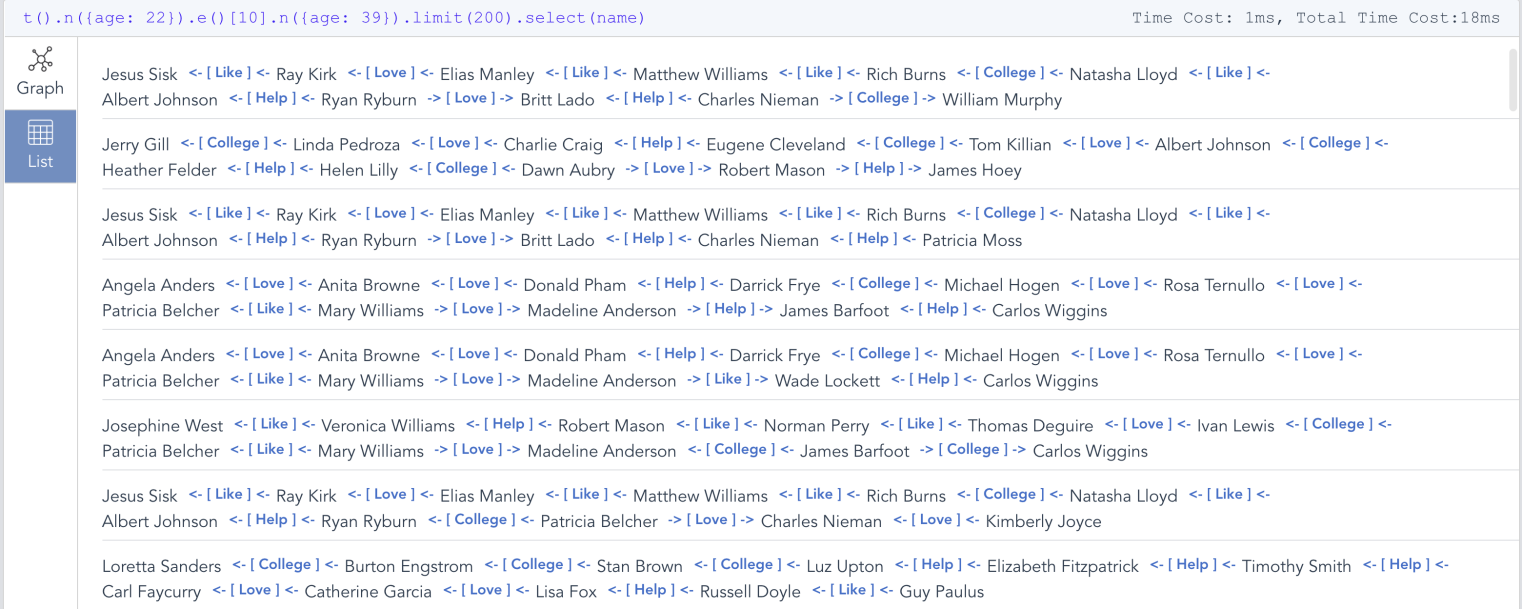
基于模板的路径查询以及路径结果的列表视图

上面那一行UQL语句已经足够不言自明：递归部分就在e()[10]，它指定搜索深度正好是 10 层；当然，您可以将其修改为 e()[5:11]，它代表从5层到11层的遍历深度；或者e()[:10]， 也就是最多10层；还可以是 e()[*:10]，其中 * 表示不超过10的最短路径（BFS）搜索：

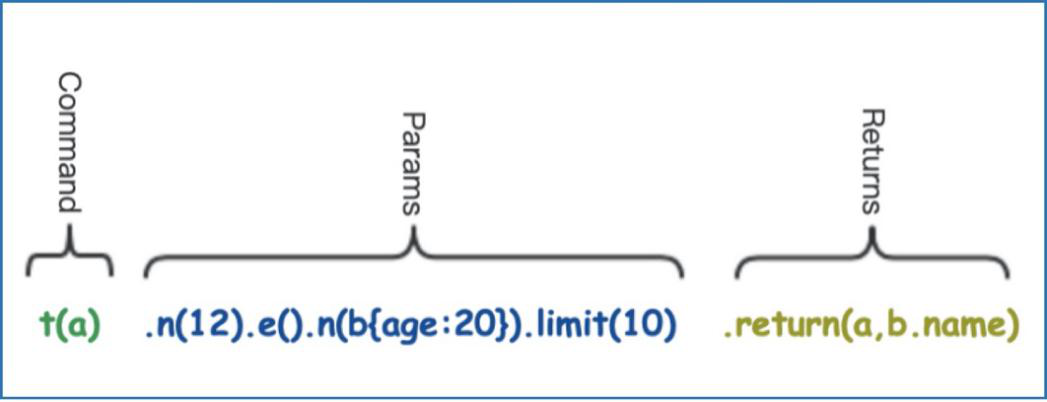
我们可以用很多方式对这种模板查询进行扩展，例如过滤边上的属性、进行数学和统计运算等。例如，仅沿着relationship =“Love”的边进行路径搜索，以下是UQL语句以及搜索结果：

t().n({age: 22}).e({name:”Love”})[3:5].n({age: 39}).limit(200).return(*)

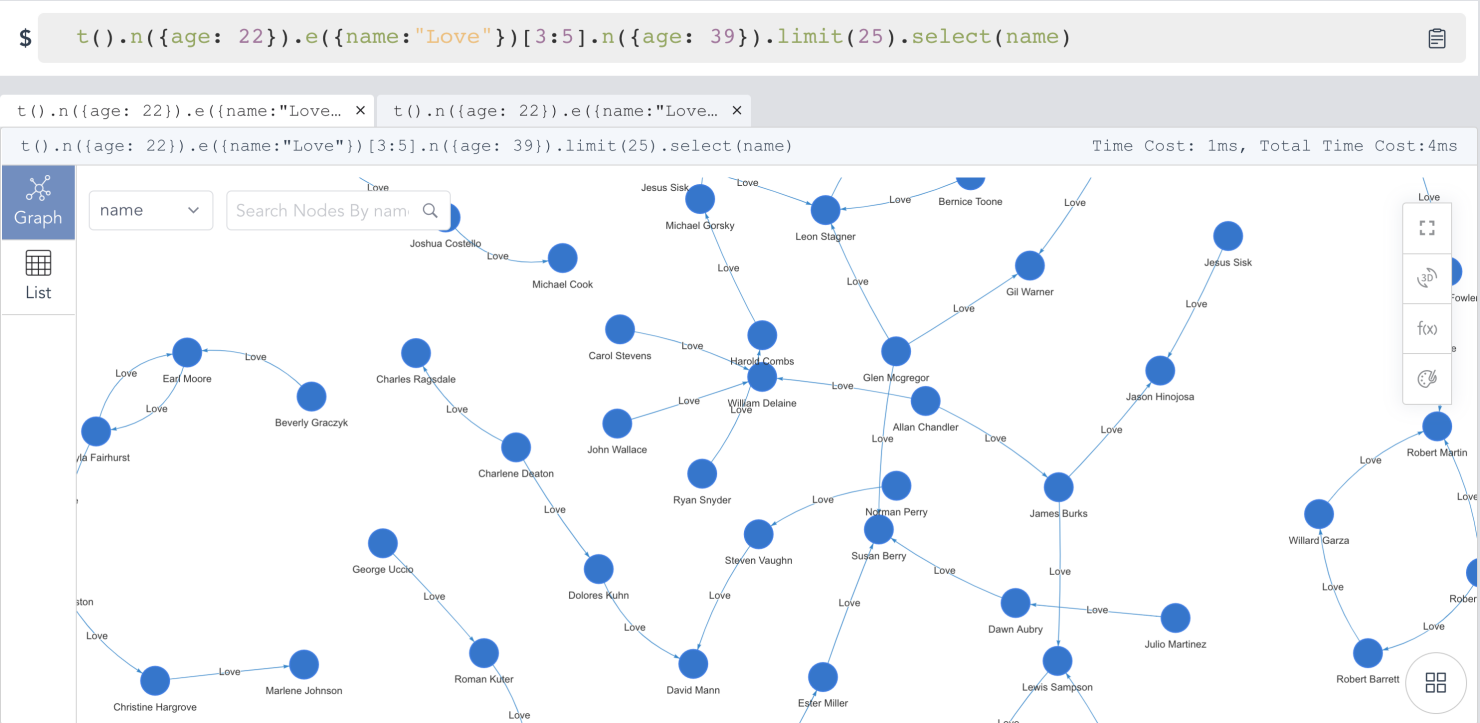
基于模板的路径查询以及路径结果的 2D 视图

简单性

借助强大的递归查询，许多事情都可以简单地完成。接下来我们将介绍一个智能推荐用例，并对比 Neo4j、TigerGraph 和嬴图各自的实现。

当今大多数由系统实现的智能推荐都类似于社交推荐——或称“协同过滤”，其本质就是通过图上的关联关系进行推荐：

向客户推荐产品时，通常的做法是首先查看该客户朋友的购物行为，然后根据调查结果给出建议…

让我们看看这3个图系统是如何应对协同过滤的。

Neo4j 用 Cypher 语言编写如下逻辑：

MATCH (customer:Customer {name: ‘Ricky Summertime’})-[:FRIEND*1..2]->(friend:Customer) WHERE customer <> friend

WITH DISTINCT friend
MATCH (friend)-[:BOUGHT]->(:Basket)<-[:IN]-(product:Product)

RETURN product, count(product) ORDER BY count(product) DESC LIMIT 5

以上逻辑解读为：

1. 查找 Ricky 的朋友，以及朋友的朋友 (第一部分)
2. 对这些朋友进行去重
3. 查找去重后的朋友购买了哪些商品 (第二部分)
4. 返回购买频率最高的 5 种商品

Neo4j 的逻辑得以实现的前提是“朋友”类型的关系必须充分的在图中标识出来，但是电商网站通常不会掌握其用户的社交关系，所以即便是像淘宝、天猫这种世界级的电商网站也无法满足 Neo4j 所假设的前提。

Neo4j 及其 Cypher 语言的另一个显著的局限性在于，它们的图遍历很浅，需要人为地将 1 ~ 2 层的遍历结果（第一部分的结果）保存为中间数据集，再进行后面步骤（第二部分）的遍历。这种尴尬在 UBO 场景（最终受益人追踪）中会变得苦不堪言—— UBO 可能会藏在 10 层、甚至是 15 层深的遮蔽之后。对这类深度遍历的应用场景，Neo4j 显然无法体面、快速的完成搜索任务。

TigerGraph 采用的是 GSQL 语言（GraphSQL 的缩写），以下为其官方文档中所介绍的实现相关功能的代码片段：

cf_query.gsql - Define the collaborative filtering query
CREATE QUERY topCoLiked( vertex<User> input_user, INT topk)
    FOR GRAPH gsql_demo
{
    SumAccum<int> @cnt = 0; # @cnt is a runtime attribute to be associated with each User vertex # to record how many times a user is liked.
    L0 = {input_user};
    L1 = SELECT tgt tFROM L0-(Liked_By)->User:tgt;
    L2 = SELECT tgt FROM L1-(Liked)->:tgt WHERE tgt != input_user ACCUM tgt.@cnt += 1 ORDER BY tgt.@cnt DESC LIMIT topk;
    PRINT L2;
}

以上代码的思路是：

1. 指定一批用户（初始用户）
2. 查找给这些用户点过赞的用户（中间用户）
3. 查找其它被这些中间用户点过赞的用户，适当聚合（ACCUM）后按一定顺序返回这些用户

要说明的是，TigerGraph 的这种“两层+聚合”的思路在我们看来并没有真正地实现“协同过滤”（最终返回的不是商品）；另外，上面的 GSQL 语句太过复杂冗长。我们知道 SQL 有一个根深蒂固的缺点就是可读性差——阅读一个超过 10 行的 SQL 语句的难度更是可想而知——很遗憾，上面这段 GSQL 代码恰恰表现出了这种缺点。

如果用UQL来实现上述的协同过滤，则只需要写：

该语句直观的表达了：

1. 从一个用户出发，到达他浏览过的商品
2. 到达购买过这些商品的用户
3. 再到达这些用户购买过的其它商品
4. 返回 10000 条这样的路径

以上UQL的查询结果如下：

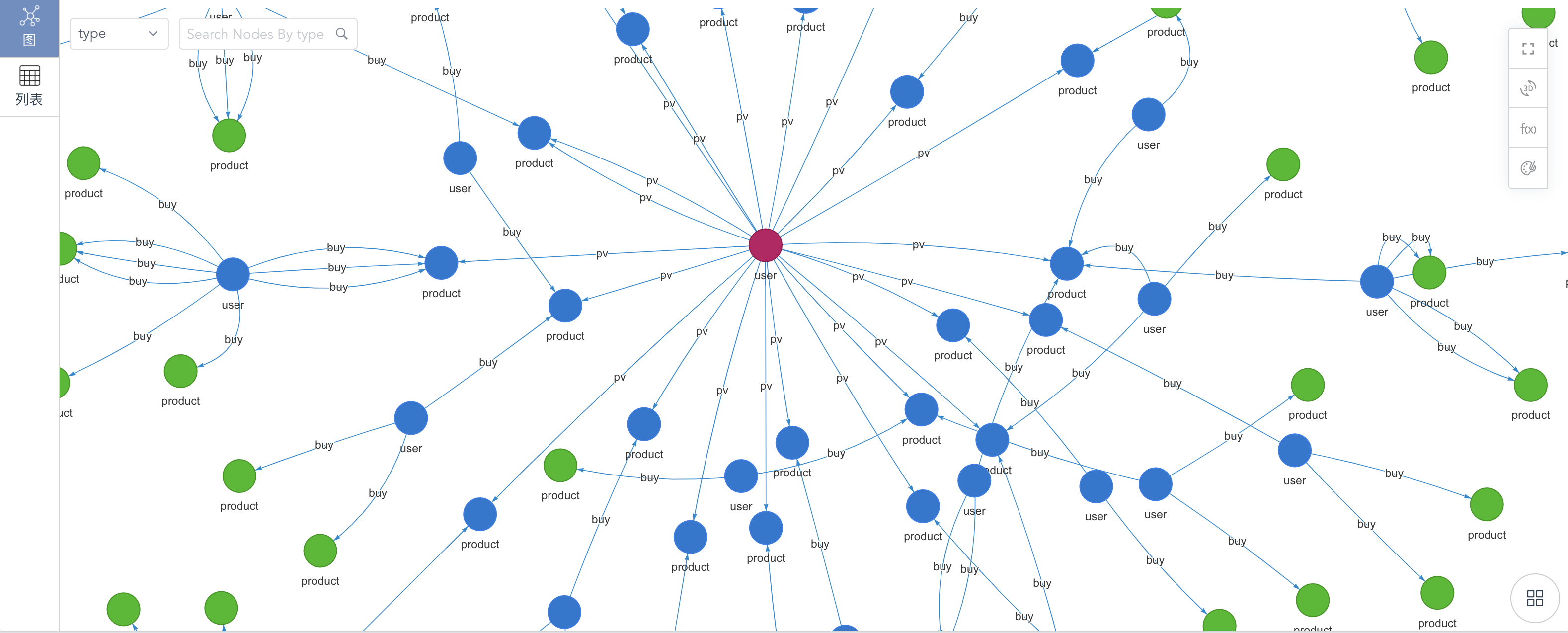
基于路径查询的协同过滤

总结

在本文中我们阐述了嬴图查询语言UQL的两大特征：

• 快速:  真正能够实时完成查询（上面举例的查询在~1ms内返回）
• 简洁:  语法及其易读且 100% 体现了人类思考方式

高级查询语言的精妙之处恰恰在于简单，而不是复杂。它应该是易于理解的，只需要最少的理解成本，而且执行起来应该是飞快的！所有繁琐的工作都应该由底层系统来承担，留给人类用户直接可见的结果。就像世界由古希腊巨神 Atlas 背负，而不会给生活在地球上的用户带来负担。

我们希望之前给出的图查询示例已经充分表明了图查询语言所应具备的特点。我们信奉的理念是：

• 要掌握图数据库查询语言只需了解业务即可，而不一定非得是数据科学家或分析师；
• 查询语言应该非常简洁易于使用，但非常强大，而对应的复杂计算工作由底层数据库引擎来封装实现；
• 最后，图数据库具有巨大的潜力可以继续发展并接替很大一部分 SQL 的应用场景。

有些人声称 RDBMS 和 SQL 永远不会被取代，但我们发现这很难相信。RDBMS 在 70 年代取代了导航数据库，并在随后的近 50 年中一直相当成功；但如果说历史教会了我们什么，那就任何事物都会消亡，推陈出新才是永恒的主流。

“What you cherish, perish”

“What you resist, persist”

如果人脑是终极的数据库，那么图数据库是到达那里的最短路径