作者：孙宇熙，王昊

在之前的几篇文章中《图数据结构的进化》与《数据库查询语言的进化》中，我们介绍了图数据结构与数据库查询语言及其发展历程，我们同时也以一种广谱的视角展示了真实场景中的图技术的相关应用。社交网络在本质上是一张图，它精准的表达了人们之间的关联关系；生物科技与制药行业通过图来了解蛋白质之间的互动关系以及化合物的药效；在供应链、电信网络、电网中，图也能天然的表达各自网络所包含的实体间的关联关系。越来越多的行业开始关注并利用图来帮助他们解决所遇到的问题。

在大数据时代，越来越多的商家、企业喜欢使用机器学习来增强它们对于商业前景的可预测性。有的采用了深度学习、神经元网络的的技术来获取更大的预测能力。但是，围绕着这些技术手段，三个问题一直萦绕不断：

• 生态中的多系统间割裂问题（Siloed Systems within AI Eco-system）
• 低性能（Low Performance AI）
• 黑盒化（Black-Box AI）

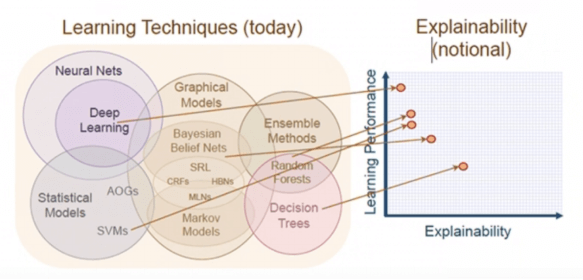
Graph-0: AI机器学习技巧以及性能&可解释性

Graph-0中就很好的呼应了上面提到的3大问题。首先，机器学习的技巧很多，从统计学模型到神经元网络，从决策树到随机森林，从马可夫模型到贝叶斯网络到图模型，不一而足，但是这么多星罗棋布的零散的模型却并没有一个所谓的一站式服务平台。大多数的AI用户和程序员每天都在面对多个、相互间割裂的、烟囱式的系统 – 每个系统都需要准备不同类型、不同格式的数据、不同的软件硬件配置，大量的ETL或ELT类的工作需要完成（后面我们会给出具体的例子）。其次，基于机器学习和深度学习的AI还面临着性能与解释性的双重尴尬，所谓的高性能的深度学习往往并不具备良好的过程可解释性，这个在各类神经元网络中体现的尤其强烈 – 人类决策者是很难容忍过程不可解释、非白盒化的AI解决方案的 – 这也是为什么在欧洲、美国、日本、新加坡等地，金融机构、政府职能部门都在推动AI技术与应用落地时的白盒化、可解释性。最后，性能问题同样的不可忽视，数据处理、ETL、海量数据的训练和验证，整个过程是如此的复杂和漫长。这些问题都是不可忽视的存在。理想状态下，我们需要基础架构层的创新来一揽子的应对并解决这些挑战。

图数据库恰好就是那个基础架构层的创新。我们在本文中会解读为什么和如何解决以上的问题。

传统意义上，数学和统计学的操作在图上面是非常有限的。要想更好的了解这个问题，我们需要先明白图数据结构的演进，在我们之前的一篇名为《图数据结构的进化》的文章中介绍了相关的信息，有兴趣的读者不妨翻阅一下。简而言之，在相邻矩阵或相邻链表类的数据结构中，很少的数学和统计学的操作可以被完成，更不用说它们大体都无法应对高并发的场景。为了解决这个挑战，我们创造性的设计了一种支持高并发的相邻哈希的数据结构，而在其之上可以支持更丰富的数学、统计学计算与操作可以算作是一个额外的红利吧——不过这是后话。

图嵌入（Graph Embedding）理念的基础是把一张属性图（Property Graph）转换到向量空间（Vector Space），因为向量空间内更多的数学、统计学的操作可以被实现和完成。这种转换实际上是把高维度数据压缩到了低维空间来表达，同时保留了一些属性，例如图的拓扑结构、点边的关系等等。这种转换还有其它的优点，例如向量操作简单、迅捷。需要指出的是，向量空间的操作所指和覆盖的是非常广泛的一大类数据结构，而上面提到的相邻哈希（adjacency hash*）也属于广义上的向量空间数据结构 – 在其之上可以实现高性能、高并发的操作。

关于相邻哈希与图数据库，我们需要向读者提供一些必要的、延展的信息。嬴图数据库通过在内存存储与计算架构中使用了”相邻哈希“实现了前所未有的高并发、高性能以及高数据处理吞吐率。当然，对于图嵌入操作而言，这种底层的向量空间数据结构天然的就是以嵌入的方式、原生图的方式存储图的基础数据（点、边、属性等），任何在此基础之上的数学、统计学计算等需求都可以更容易实现。而当我们在数据结构、基础架构以及算法的工程实现层面都做到了可以充分的释放和利用底层硬件的并发能力的时候（例如对CPU的内核的充分利用——在一台双CPU的X86 PC服务器架构中，超线程数可达112，也就是说如果全部100%并发，CPU的全速、满负荷运行%为：11,200%，而不是100%！！遗憾的是，相当多的互联网后台开发程序员试图想证明当他们不能让1台服务器跑满的情况下，可以通过多机的分布式系统来实现更高的计算效率，这是典型的本末倒置——我们当然要先把1台机器的并发能力释放出来后，才会以水平可扩展的方式去释放第二台、第三台的算力…），在图上的很多原来非常耗时的图嵌入的操作就可以以非常高效和及时的方式完成。

下面，让我们通过Word2Vec的例子来解释为什么图嵌入类的操作在嬴图数据库上可以跑的更快，也更简洁（例如：轻量级存储、过程可解释）。Word2Vec方法可以看做是其它面向顶点、边、子图或全图的图嵌入方法的基础。简而言之，它把单词（word）嵌入（转换）到了向量空间 – 在低维向量空间中，意思相近的单词有着相似的嵌入结果。著名的英国语言学家J.R. Firth在1957年曾说过：你可以通过了解一个单词的邻居（上下文）而了解这个单词。也就是说，具有相似含义的单词倾向于具有相似的近邻单词。

在以下的三张配图（Graph-1/2/3）当中，介绍了实现Word2Vec所用到的算法和训练方法：

• Skip-gram算法
• Softmax训练方法

还有其它的算法，例如Continuous Bag of Words和方法，例如Negative Sampling（负取样）等。

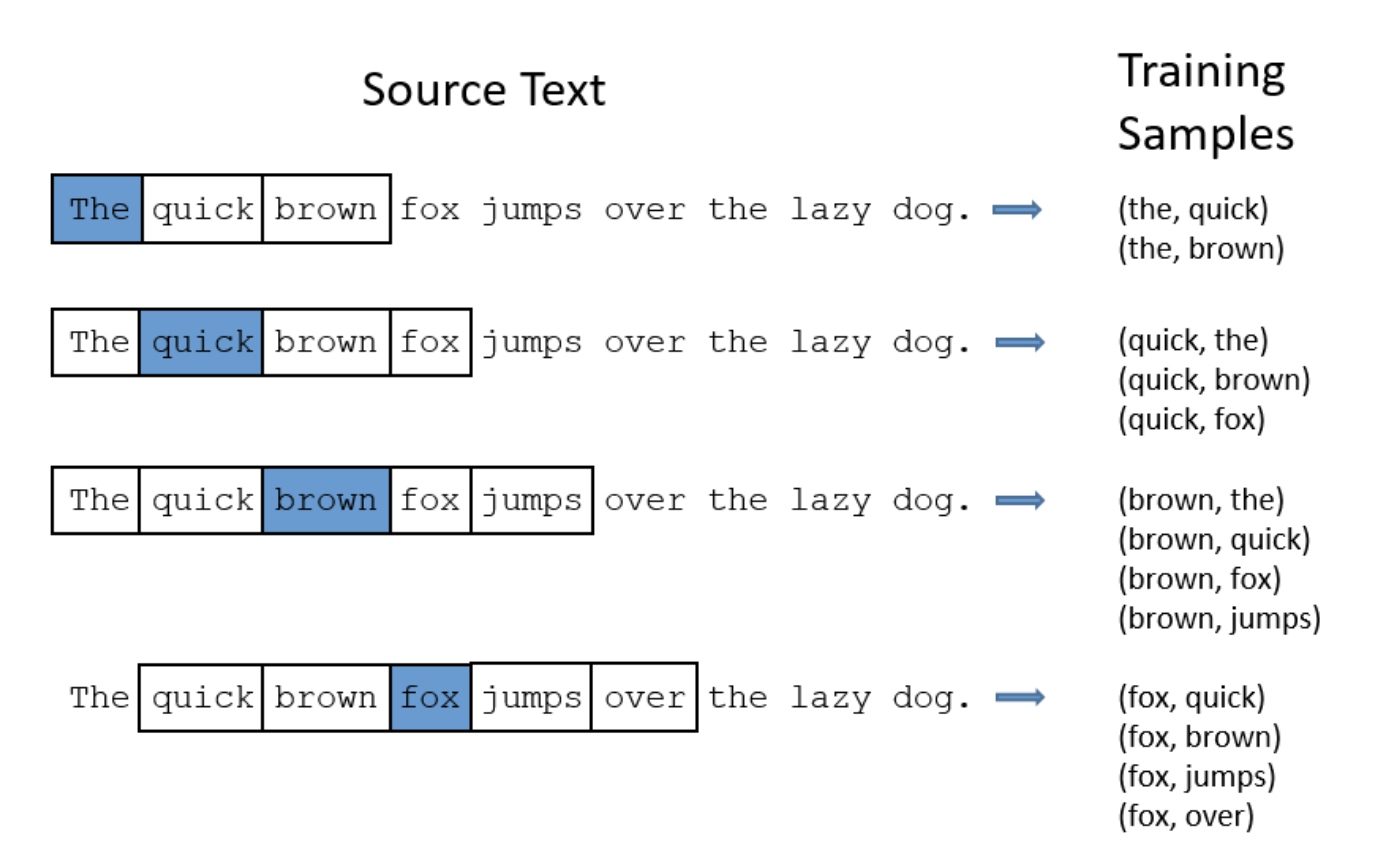
Graph-1: Word2Vec从原文到训练采样数据集

Graph-1中展现的是当采样窗口大小为2的时候（意味着每个当前关注、高亮的单词的前两个和后两个相连的单词会被采样），采集到的样本集的效果。注：在改进的Word2Vec方法中，Subsamplings技术被用来去除那些常见的单词，例如“the”，并以此来提高整体的采样效果和性能。

为了表达一个单词并把它输入给一个神经元网络，一种叫做one-hot的向量方法被使用到了，如图Graph-2所示。输入的对应于单词ants的one-hot向量是一个有1万个元素的向量，其中只有一个元素为1（对应为ants），其它元素为全部为0。同样的，输出的向量也包含1万个元素，但是包含着每一个近邻的单词出现的可能性。

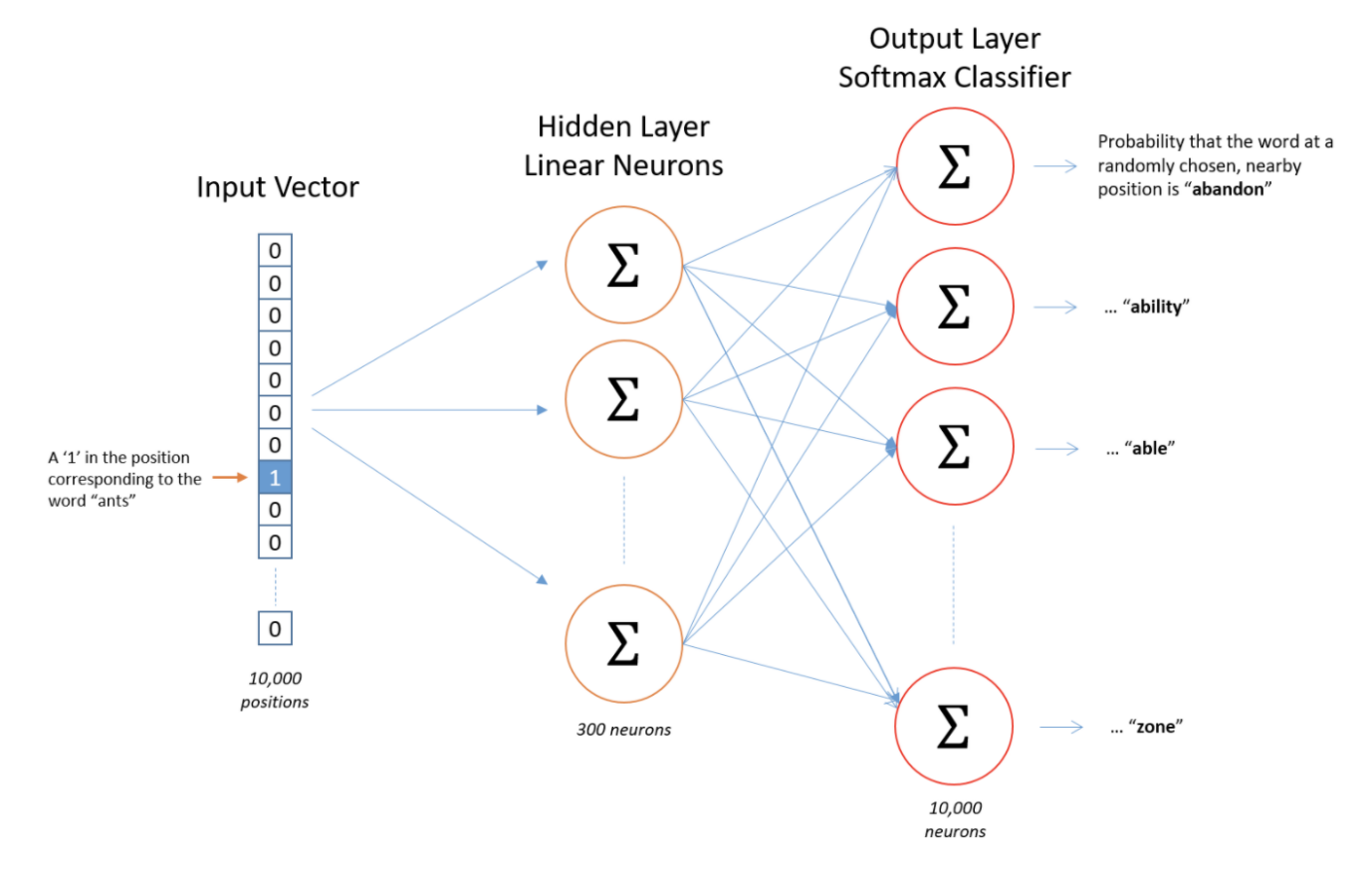
Graph-2: Word2Vec神经元网络架构示意图

假设我们的词汇表中只有1万个单词，以及对应的300个功能（features）或者是可以用来调优Word2Vec模型的参数。这种设计可以理解为对应着一个10,000*300的二维矩阵，如下图Graph-3所示，在隐藏层（hidden layer）中的300个神经元。

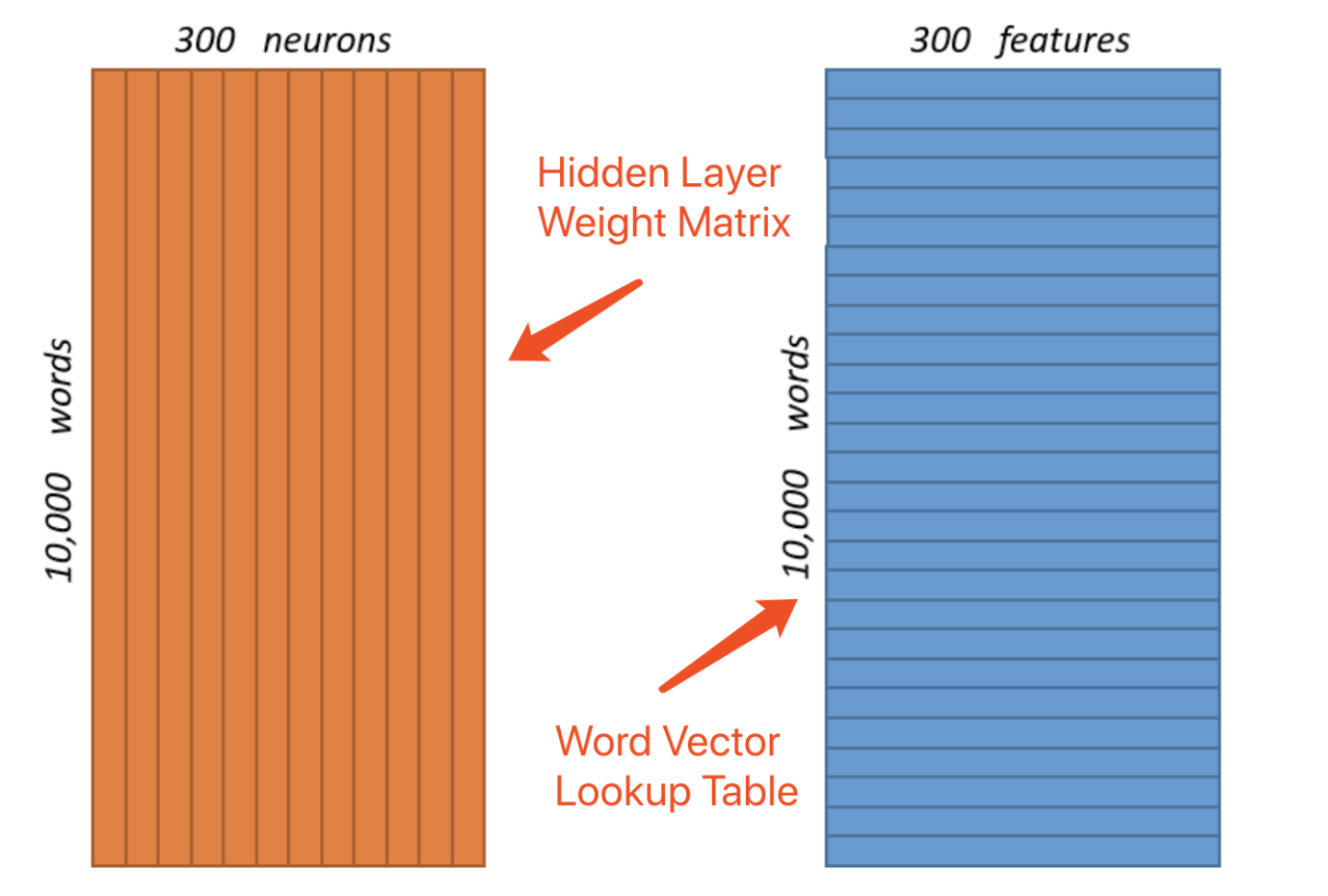
Graph-3: 巨大的单词向量 (3,000,000 Weights!)

从上图中可以看到，隐藏层和输出层每个都负载着权重达3,000,000的数据结构。对于真实世界中的应用场景，词汇数量可能多达数百万，每个单词有上百个features的话，one-hot的向量会达到数以十亿计，即便是使用过了sub-sampling、negative-sampling或word-pair-phrase等（压缩）优化技术，计算复杂度也是不可忽略的。很显然，这种one-hot向量的数据结构的设计方式过于稀疏了，它很像相邻矩阵。同样的，利用GPU尽管可以通过并发来实现一定的运算加速，但是对于巨大的运算量需求而言依然是杯水车薪（低效）。

现在，让我们回顾Word2Vec的诉求是什么？我们想要预测，在一个搜索与推荐系统中，当一个单词（或多个）被输入的时候，我们希望系统给用户推荐什么其他单词？对于计算机系统而言，这是个数学-统计学（概率）问题：有着最高可能性分值的单词，或者说最为近邻的单词，会被优先推荐出来。从数据建模的角度上来看，这个挑战是典型的图计算挑战！当一个单词被看做是图中的一个顶点的时候，它的邻居（和它关联的顶点）是那些经常在自然语句中出现在它前后的单词 – 这个逻辑可以以递归的方式延展开来，进而构成一张自然语言中的完整的图。每个顶点、每条边都可以有它们各自的属性、权重、标签等等。

上文中描述的图的存储结构可以对应于下图（Graph-4）。我们设计了两种基于相邻哈希的数据结构，表面上看它们类似于Big-Table，但是在实现层，通过高并发架构赋予了这些数据结构超高的无索引查询（Index-Free Adjacency）可计算性能。

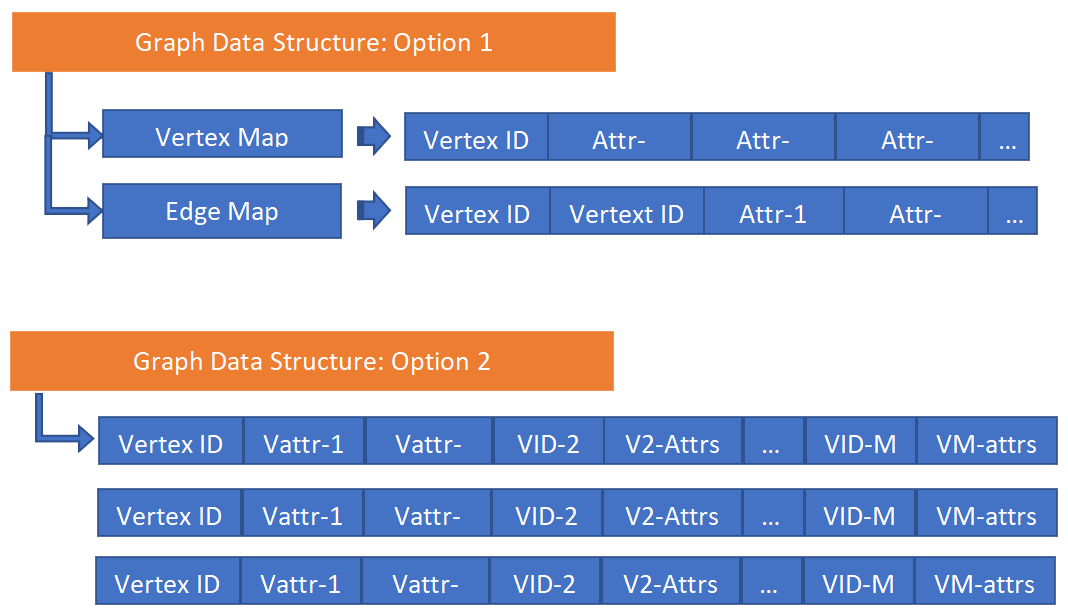
Graph-4: 原生支持图嵌入的图数据结构

基于相邻哈希（adjacency hash*）数据结构，Word2Vec问题可以被分解为如下两个清晰（但是并不简单）的步骤：

• 为图中每个关联两个单词（顶点）的有向边赋值一个“可能性”权重 – 这个可以通过基于统计分析的预处理的方式实现。
• 搜索和推荐可以通过简短的图遍历操作来实现，例如对于任何出发的单词（顶点），查询并返回前X个数量的邻居顶点。该操作可以以递归的方式在图中前进，每次用户选定一个新的顶点后，就会实时的进行新的推荐。当然也可以进行深度的图路径计算以实现出类似于返回一个完整的、长句子的推荐效果。

上面的第二步中的描述非常类似于一套实时搜索系统&推荐（suggestion）系统，并且它的整个的计算逻辑就是人脑是如何进行自然语言处理（NLP）的白盒化过程。

上面我们描述的就是一个完整的白盒化的图嵌入的处理过程。每一个步骤都是确定的、可解释的、清晰的。它和再之前的那种黑盒化和带有隐藏层（多层）的方法截然不同（参考配图Graph-2、3）。这也是为什么我们说深度的实时图计算技术会驱动XAI的发展 – XAI = 可解释的人工智能（eXplainable AI）。

相邻哈希数据结构天然的就采用图嵌入的方式构造 – 当图中的数据通过相邻哈希的结构被存储后，嵌入的过程就自然而然的完成了，这也是相邻哈希类原生图存储在面向图嵌入、图神经网络时的一个重要优势。

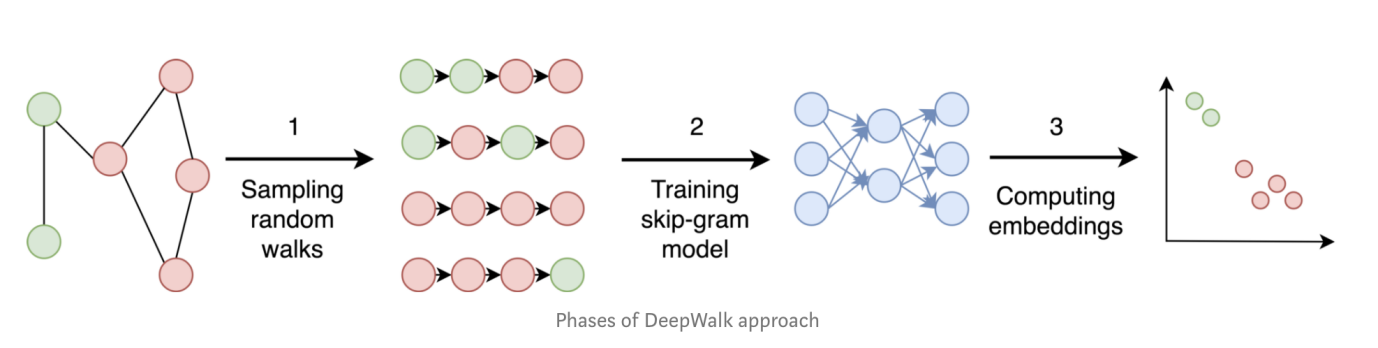
Graph-6: 深度游走（DeepWalk）的步骤分解

让我们来看第二个例子：DeepWalk（深度游走）。它是一个典型的以顶点为中心的嵌入方法，通过随机游走（random walks）来实现嵌入过程。利用相邻哈希，随机游走的实现极为简单 – 仅仅需要从任一顶点出发，以随机的方式前往一个随机相邻的顶点，并把这个步骤以递归的方式在图中深度的前行，例如前进40层（步）。需要注意的是，在传统的计算及IT系统中（包含所有的在嬴图之前的传统的图数据库），通常来说每一层深入查询或访问都意味着计算资源的消耗是指数级的增加 – 如果平均每个顶点有20个邻居，查询深度为40层的计算复杂度为：20⁴⁰，没有任何已知的系统可以以一种实时或近实时的方式完成这种暴力运算任务。但是，得益于相邻哈希数据结构，我们知道每一层的顶点可以以并发的方式去访问它的相邻顶点，时间复杂度为O(1)，然后每个相邻顶点的下一层邻居又以并发的方式被分而治之，如果有无穷的并发资源可以被利用，那么理论上的深度探索40层的时间复杂度为O(40*20) – 当然，实际上计算并发资源是有限的，因此时间复杂度可能会高于O(800)，但是可以想见，会远远低于 O(20⁴⁰)！

Graph-6中示意的是典型的深度游走的步骤。利用相邻哈希，随机游走、训练和嵌入过程被降解为原生的图操作，例如K-邻和路径查询操作 – 这些操作都是直观、可解释的，也就是说是XAI友好的！

深度游走（DeepWalk）在学术界和业界经常被批评缺少通用性（普适性），它没有办法应对那种高度动态的图。例如，每个新的顶点（及边）出现后都要被再次训练，并且本地的邻居属性信息也不可以被保留。

Node2Vec被发明出来就是要解决上面提到的DeepWalk非通用性中的第二个问题。Graph-7中展示了整个学习过程的完整的步骤 – 10步（含子进程），其中每个步骤又可以被分解为一套冗长的计算过程。传统意义上，像Node2Vec类的图嵌入方法需要很长时间（以及很多的资源，例如内存）来完成（用过Python的读者可能会更有体会！），但是，嬴图数据库的图嵌入AI算法集把这些步骤都进行了高并发改造，通过高效的利用和释放底层的硬件并发能力来缩短步骤执行时间。如下的进程都被改造为并发模式了：

• Node2Vec随机游走（random walks）
• 准备预计算 Table
• 词汇学习 (from Training File)
• 剔除低频词汇Low-Frequency Vocabularies
• 常见单词（vectors）的Sub-sampling
• 初始化网络 (Hidden Layer, Input and Output Layers)
• 初始化Unigram Table (Negative Sampling)
• Skip-Gram训练

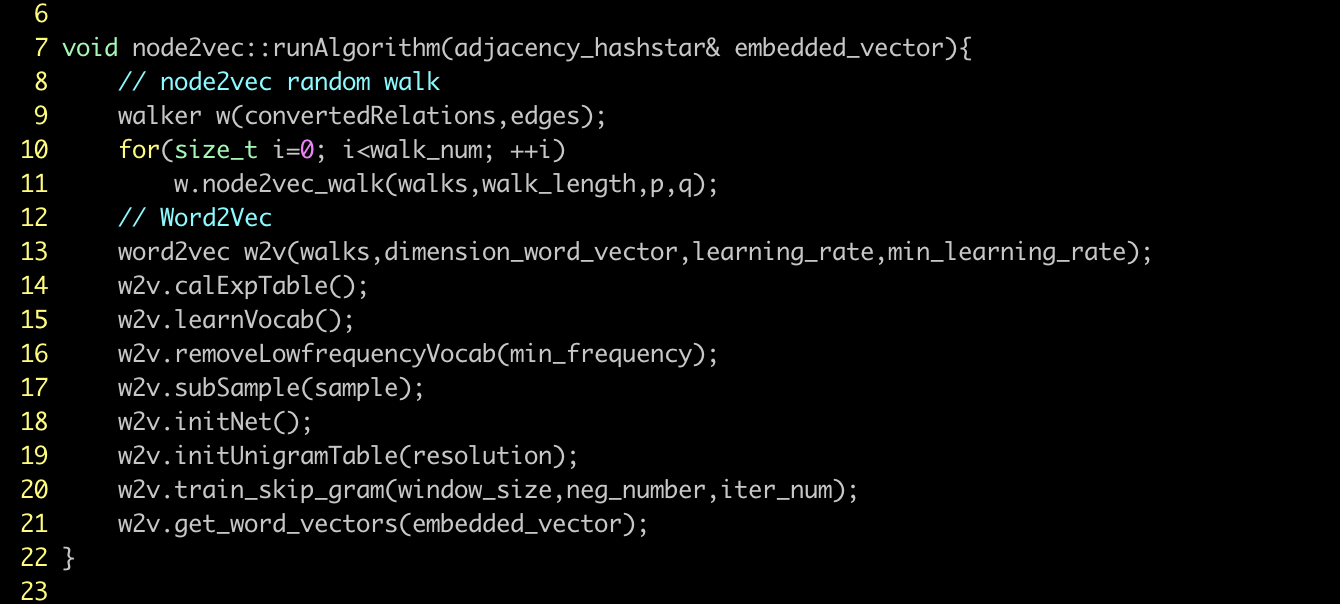
Graph-7: Outer Steps of Node2Vec Relying on Word2Vec

通过高度的并发实现，我们实现了高性能与低延迟。值得指出的是：每一秒钟没有实现高并发的运算，对于底层的计算（或存储、网络）资源而言都是一种浪费 – 是对环境污染的一种漠视 – 对于环保或者计算资源的充分并发，我们是严肃、认真的。

还有其它的图嵌入技巧具有相似的理念和步骤，例如：

• 取样和标签（Sampling and labeling）
• 模型训练（e., Skip-Gram, n-Gram, and etc.)
• 嵌入计算（Computing embeddings）

有些计算需要在顶点或子图级别完成，有些则需要对全图进行运算，因此也会因计算复杂度的指数级增加而耗费更多的计算资源。无论是哪一种模式，可以实现以下的效果将会是非常美妙的：

1. 在数据结构、架构和算法实现层面实现高性能、高并发；
2. 每一步的操作都是确定、可解释的以及白盒化的；
3. 理想状态下，每个操作都以一站式的方式完成（连贯的、统一的，无需数据迁移或反复转换的）。

现在，让我们回顾本文开头的地方，Graph-0所触及的可解释性vs.性能的问题。决策树有着较好的可解释性，因为我们明白它每一步在做什么，树在本质上就是简单的图，它并不包含环路、交叉环路这种数学（计算）意义上复杂的拓扑结构 – 因为后者更难解释，当这种高难度的不可解释性层层叠加后，整个系统就变成了一个巨大的黑盒，这也是我们今天的很多AI系统所面临的真实的窘境 – 试问人类可以忍受一套又一套的AI系统在为我们服务的时候，始终以黑盒、不可解释的方式存在吗？例如通过AI来实现的人脸识别或者小微贷款额度计算，即便在10亿人身上经过认证它是准确的，你如何能确保在下一个新用户出现的时候它是准确的且公正的呢？只要人类不能精准、全面的回溯整个所谓的AI计算过程，这种风险就一直存在。不可解释的AI，注定是不会长久的，即便在一定时期内它可能还很火爆。

今天市面上绝大多数的图算法和图嵌入实现都采用了或者性能不友好的相邻链表，或者空间不友好但是论文友好的相邻矩阵的方式来实现。不得不说，在XAI的方向上，有着巨大的IT系统的升级换代的空间与机遇。

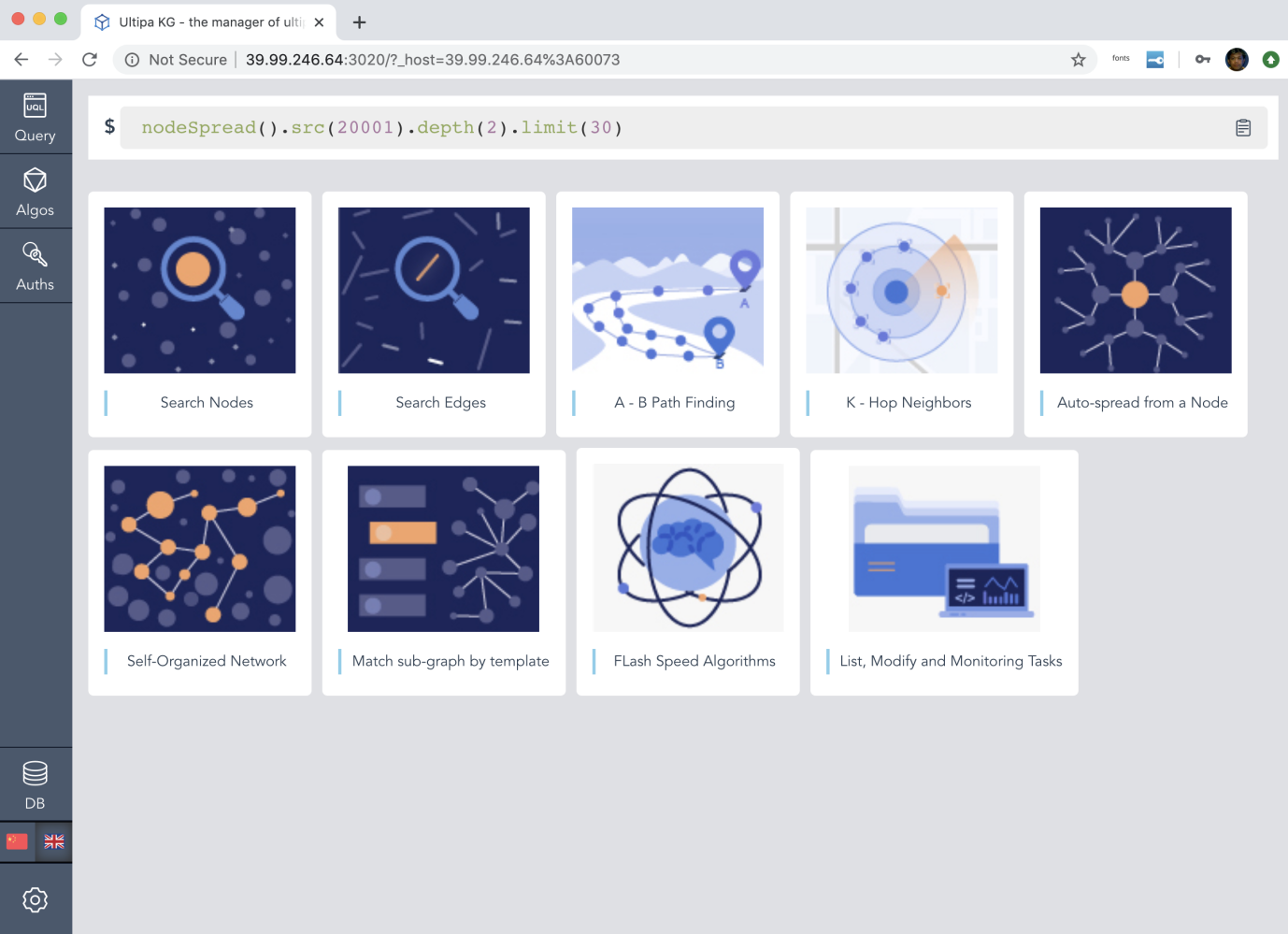
Graph-8: 一体化的嬴图实时图数据库与知识图谱管理平台

通过实现高性能、高并发的图数据结构与系统框架，我们做到了实现前文提到的3个预期的效果。在后续的文章中，我们会介绍更多的基于嬴图中台（图数据库、图计算-存储引擎）实现的XAI的功能。

在Graph-8和Graph-9中，我们展示了嬴图的前端可视化界面。前者是以表单化的方式支持用户进行图上的各类操作（搜点、搜边、搜路径、搜K邻、自动展开、多节点自动组网、模板搜索、全文本搜索、丰富的图算法以及数据库管理操作）；后者展示了一种以3D（WebGL）高可视化的方式展示图谱（子图）的空间拓扑结构。

Graph-9: 3D模式的知识图谱管理前端（嬴图Manager）

图是用来表达高维空间的，电脑屏幕是2维的，但是大脑是以高维的方式处理信息的。图数据库、图中台、图计算引擎是最忠实的还原高维空间表达的终极方案。如果人脑是终极数据库，那么图数据库是迈进终极数据库的最短路径！