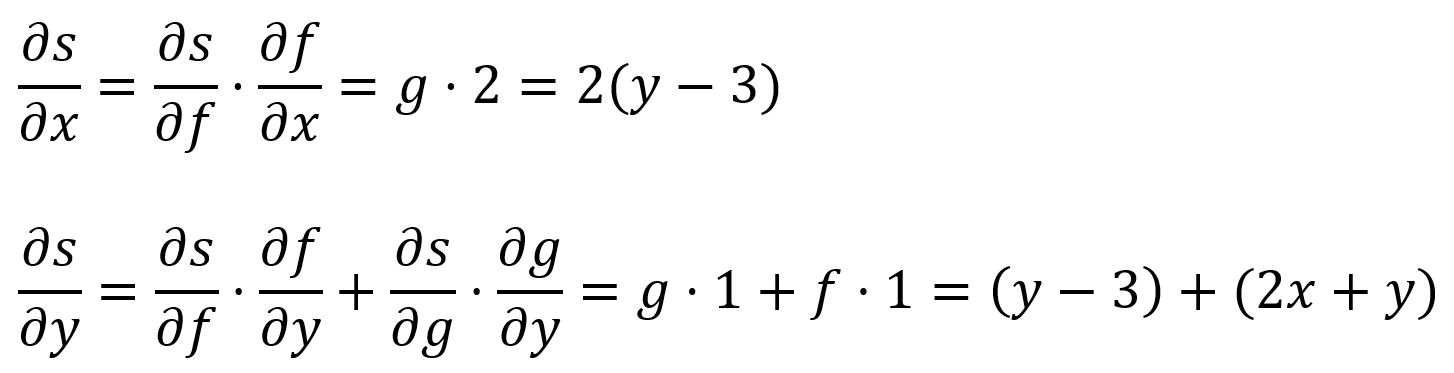梯度下降(Gradient Descent)是一种在图嵌入中广泛使用的基本优化算法。其主要目标是通过迭代调整图嵌入模型的参数,使得预定义的损失或成本函数的值最小。
梯度下降有不同的变体,每个变体都针对大规模图嵌入任务中的特定挑战进行了优化。主要的变体包括随机梯度下降(SGD, Stochastic Gradient Descent)和小批量梯度下降(MBGD, Mini-Batch Gradient Descent)。这些变体在每次迭代中只使用从单个数据点或小批量数据点计算的梯度来更新模型的参数。
基本形式
考虑一个现实场景:一个人站在山顶,希望尽快下山。一条最佳的下山路径自然是存在的,但想要精确地一下子找出这条路径却很不容易。更常见的做法是走一步看一步:每走一步到达一个新位置时,计算该位置最陡的下降方向(即梯度下降方向),然后朝着那个方向移动至下一位置。重复这个过程,直到到达山脚。
梯度下降就是一种不断沿着梯度下降方向寻找函数最小值的技术。相反地,梯度上升(Gradient Ascent)技术就是要沿着梯度上升方向找到最大值。
给定一个函数,梯度下降的基本形式是:
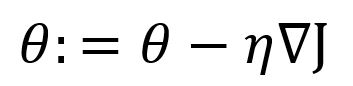
其中,是函数在位置处的梯度,是学习率(Learning Rate)。由于梯度实际上是最陡的上升方向,所以在前加一个减号就得到最陡的下降方向。
学习率决定了沿梯度下降方向朝目标前进的每一步的步长。在下山的例子中,可以将学习率视为每一步所行的距离。
在模型训练的过程中,学习率通常保持恒定。然而,有些模型的优化也可能包括学习率,例如使学习率随着训练的进行而逐渐减小或按照预定义的其他计划进行调整。这些调整旨在增强收敛性和优化效率。
示例:单变量函数
对于函数,它的梯度(在这种情况下,与导数相同)是。
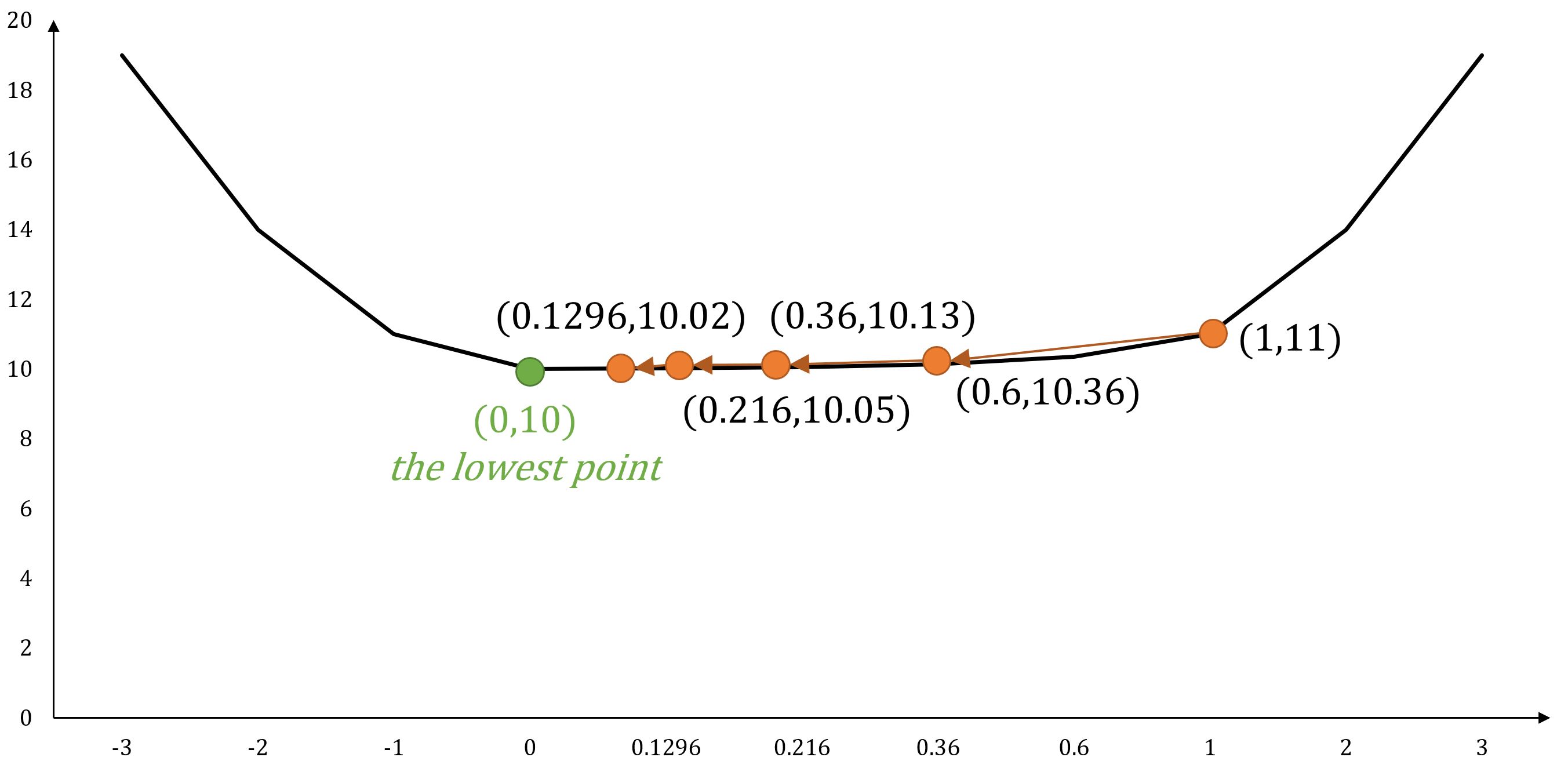
如果从的位置开始,并设置,以下是根据梯度下降原则的位置移动:
- ...
- ...
随着步数的增加,会逐渐收敛到的位置,最终达到函数的最小值。
示例:多变量函数
对于函数,其梯度是。
如果起始位置是,并设置,以下是根据梯度下降原则的位置移动:
- ...
- ...
随着步数的增加,会逐渐收敛到的位置,最终达到函数的最小值。
在图嵌入中的应用
在图嵌入的神经网络模型训练过程中,通常会使用一个损失或成本函数来评估模型的输出与预期结果之间的差异,然后应用梯度下降技术来最小化这个损失函数。这就涉及到在梯度的反方向上迭代调整模型的参数,直到收敛,从而优化模型。
为了在计算效率和准确性之间取得平衡,在实际中采用了几种梯度下降的变体,主要包括:
- 随机梯度下降 (SGD)
- 小批量梯度下降 (MBGD)
示例
考虑使用个样本来训练一个神经网络模型的场景。每个样本包括输入值和对应的期望输出。我们使用和()分别表示第 个输入值和期望的输出。
模型的假设函数(hypothesis)定义如下:
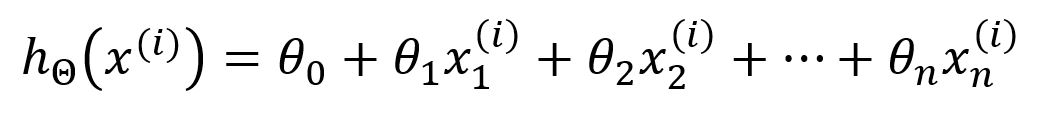
在这里,代表模型的参数 ~ ,是第个输入向量,包含个特征。模型通过函数对输入的特征进行加权组合来计算输出。
模型训练的目标是找到尽可能使得输出接近期望值的的最佳参数组合。在训练开始时,随机初始化所有参数。
在模型训练的每轮迭代中,计算出所有样本的输出后,使用均方误差(MSE)作为损失/成本函数来衡量每个输出与其对应的期望值之间的平均误差:
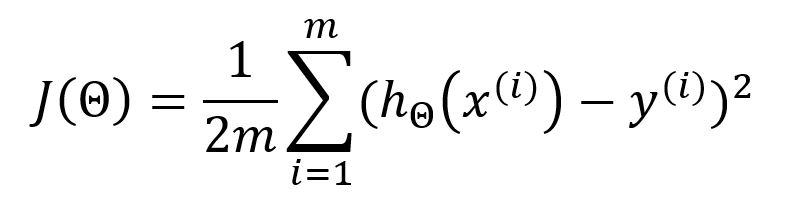
在标准的均方误差(MSE)公式中,分母是。然而,其作为机器学习的损失函数时,通常使用作为分母,目的是抵消掉对损失函数的平方项求导后产生的常数系数,从而简化后续计算。这种修改不会影响最终的结果。
随后,利用梯度下降更新参数。对求偏导数如下:
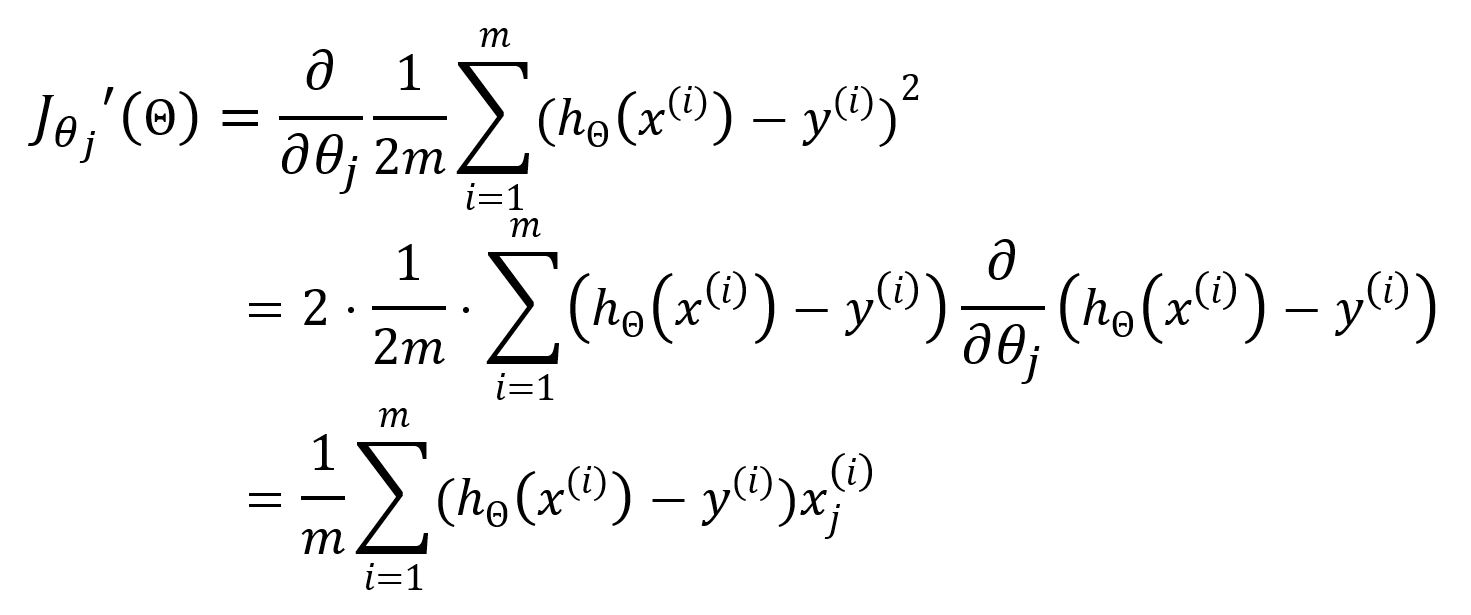
因此,更新为:
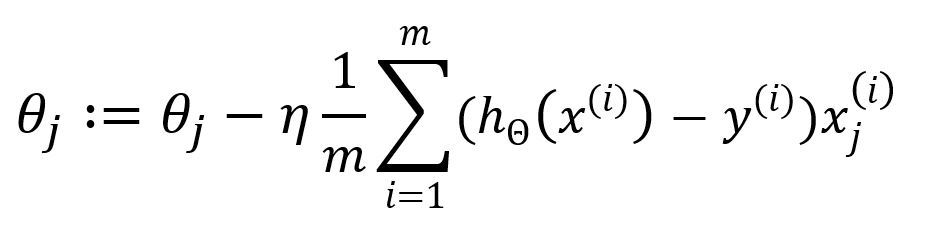
从到的求和表示在每次迭代中使用所有个样本来更新参数,这种方法被称为批量梯度下降(Batch Gradient Descent,BGD),是梯度下降优化的原始和最直接形式。在BGD中,每次迭代使用整个样本数据集来计算损失函数的梯度。
尽管BGD可以确保精确收敛到损失函数的最小值,但对于大型数据集来说计算则过于密集。因此梯度下降的变体,如SGD和MBGD,就被开发出来以平衡效率和收敛速度。它们在每次迭代中只使用训练数据的子集,使得优化过程更快,同时仍能够找到最优的参数。
随机梯度下降法
随机梯度下降(SGD)每次迭代只随机选择一个样本进行梯度计算。
在使用SGD时,上述的损失函数应表示为:
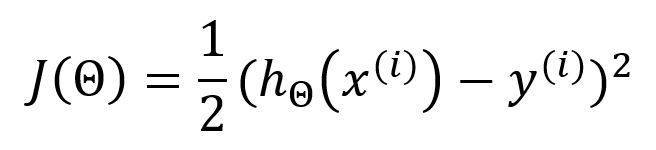
对于求偏导数为:
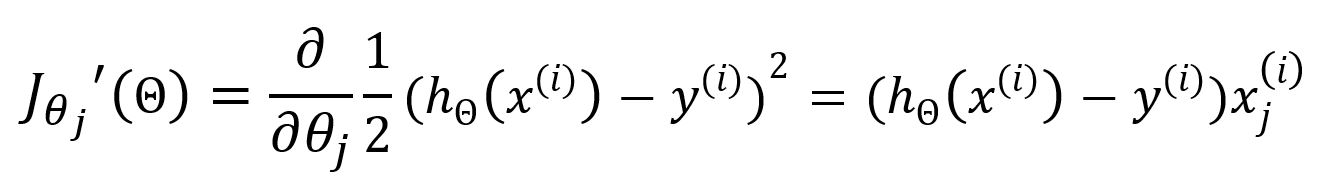
更新为:
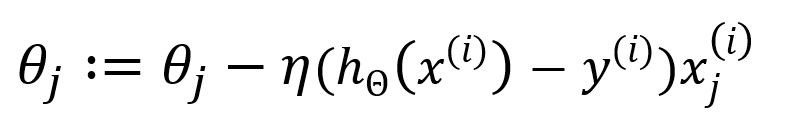
SGD的计算复杂性大大降低了,因为它只使用一个样本,不需要求和以及求平均。虽然提高了计算速度,但代价是牺牲一定程度的准确性。
小批量梯度下降法
BGD和SGD代表两个极端——一个使用所有样本,另一个只使用一个样本。小批量梯度下降法(MBGD)则随机选择大小为的样本量进行计算,以求在二者之间取得平衡。
数学基础
导数
单变量函数的导数(Derivative)通常表示为或,它表示在给定位置上略微变化时的变化。
从图上看,对应函数曲线的切线(Tangent Line)的斜率。点处的导数是:
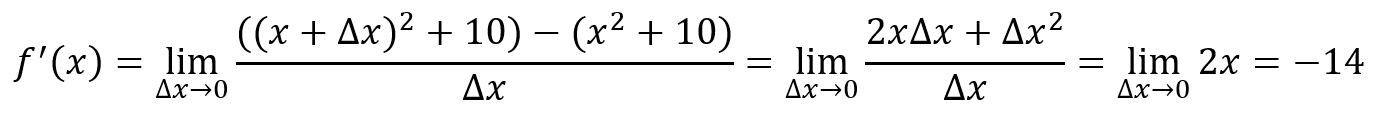
例如,,在点处:
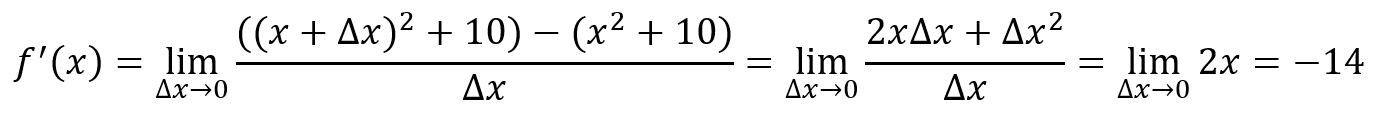
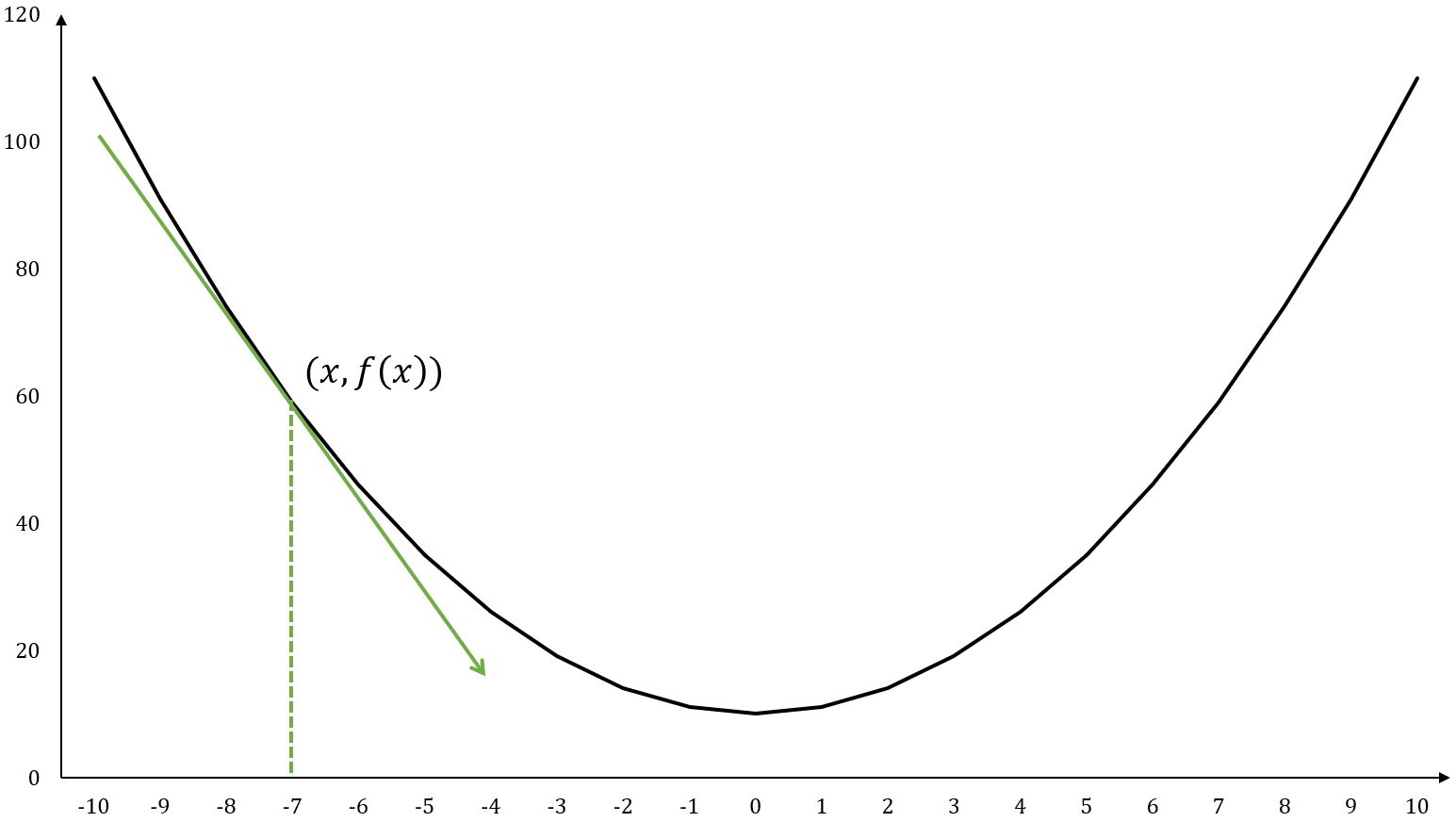
切线是指一条刚好触碰到函数曲线上某一点的直线,切线的方向与该点的方向相同。
偏导数
多变量函数的偏导数(Partial Derivative)衡量在保持其他所有变量不变的情况下,某一个变量变化时函数如何变化。对于一个函数,在特定点处,它相对于的偏导数表示为或:
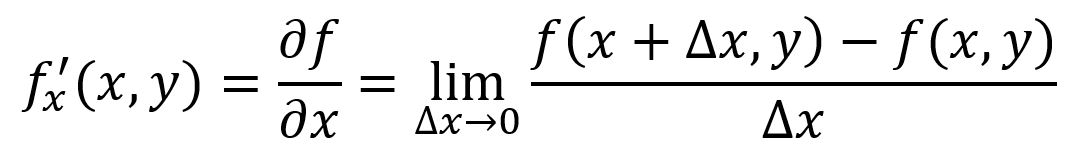
例如,,在点,处:
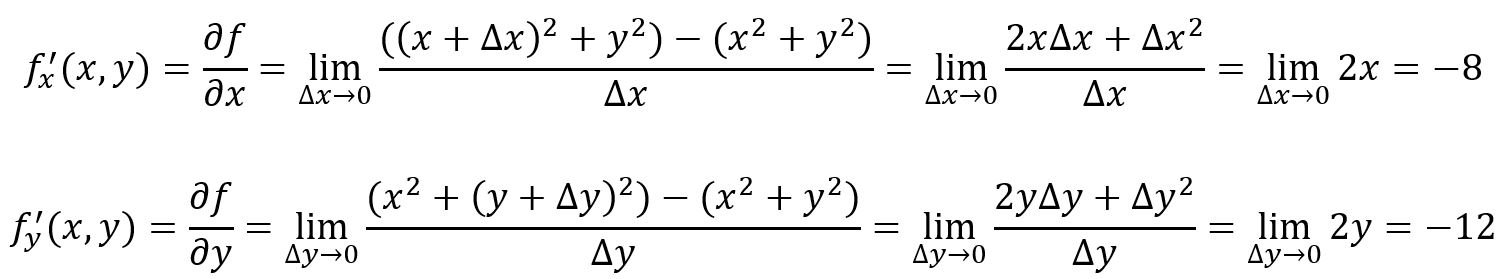
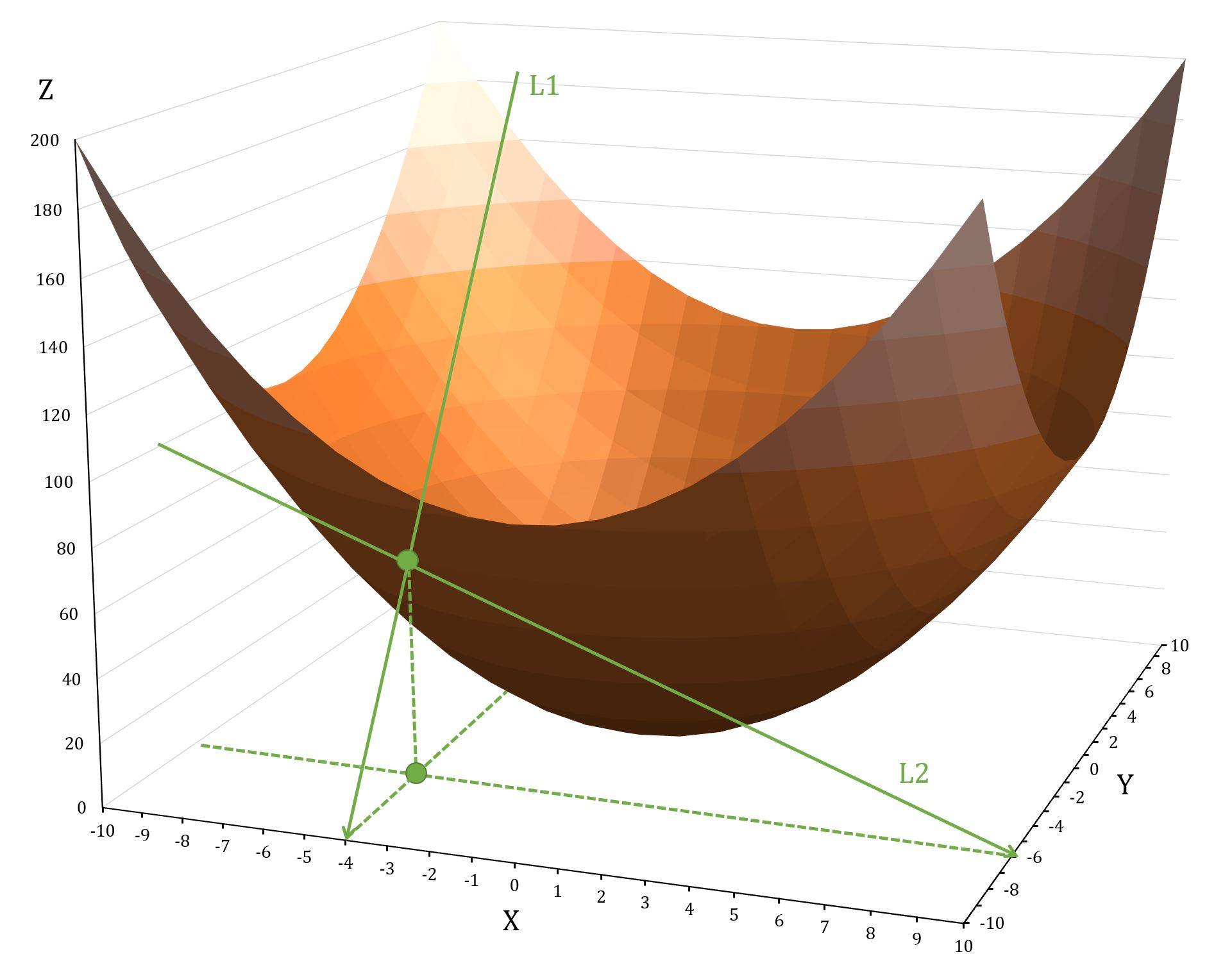
表示在保持不变、沿Y轴移动时函数的变化;表示在保持不变、沿X轴移动时函数的变化
方向导数
函数的偏导数表示沿着坐标轴方向轻微移动时输出的变化情况。当沿着与任何坐标轴都不平行的方向移动时,就有了方向导数(Directional Derivative)的概念。
方向导数在数学上表示为向量(它由函数的所有偏导数组成)与表示变化方向的单位向量 的点积:
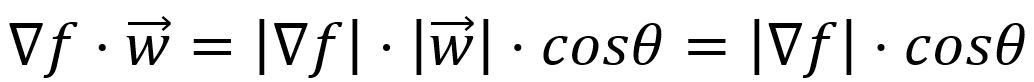
其中,是两个向量之间的夹角,并且
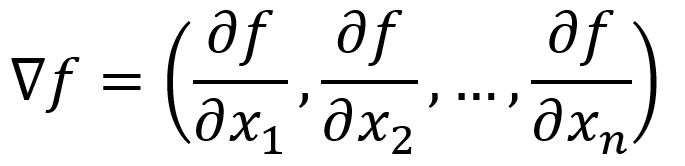
梯度
梯度(Gradient)是使函数的输出具有最陡上升的方向,这等同于找到最大的方向导数,而这发生在向量和之间的角度为时,因为,即与的方向一致。因此,就是函数的梯度。
很显然,负梯度就是函数最陡下降的方向。
链式法则
链式法则(Chain Rule)描述如何计算复合函数的导数。在最简单的形式中,复合函数的导数可以通过将关于的导数与关于的导数相乘来计算:
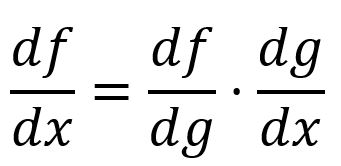
例如,由和组成,那么:
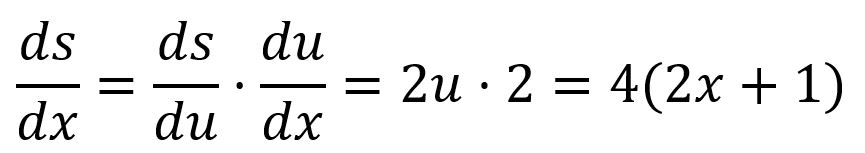
在多变量复合函数中,可以通过对每个变量应用链式法则来获得偏导数。
例如,由 以及和组成,那么: