反向传播（Backpropagation）算法的全称是误差反向传播（Error Backward Propagation）算法，是用于训练图嵌入模型的核心技术。

反向传播算法包括两个主要阶段：

• 前向传播：输入数据进入神经网络或模型的输入层，然后通过一个或多个隐藏层，最终从输出层生成输出。
• 反向传播：将生成的输出与实际或期望值进行比较。随后，将错误从输出层传递到隐藏层，然后到输入层。在这个过程中，使用梯度下降技术来调整模型的权重。

迭代调整权重的过程就是神经网络的训练过程。我们将通过具体的示例进一步解释。

准备工作

神经网络

神经网络（Neural Network）一般依次由一个输入层（Input Layer）、一个或多个隐藏层（Hidden Layer）和一个输出层（Output Layer）构成。我们构造如下简单的神经网络:

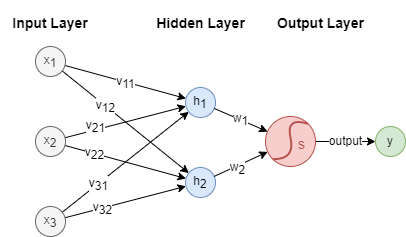
在这个示例中，$x$ 是包含 3 个特征的输入向量，$y$ 是输出。隐藏层中有两个神经元（Neurons）$h_1$ 和 $h_2$。在输出层中应用 Sigmoid 激活函数。

此外，层与层之间的连接由权重来描述：$v_{11}$ ~ $v_{32}$ 是输入层和隐藏层之间的权重，$w_1$ 和 $w_2$ 是隐藏层和输出层之间的权重。这些权重在神经网络内部的计算中起着关键作用。

激活函数

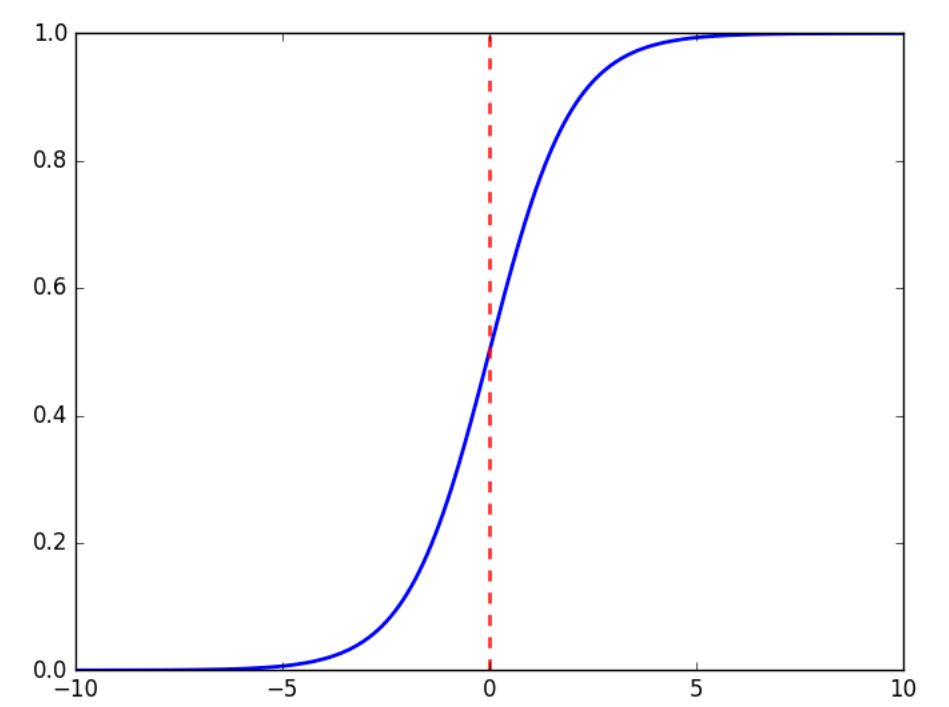
激活函数（Activation Function）为神经网络提供非线性建模的能力。如果没有激活函数，那么模型只能表达线性映射，从而限制了它们的能力。不同的激活函数有不同的作用。示例中使用的Sigmoid 函数的公式和图像表示：

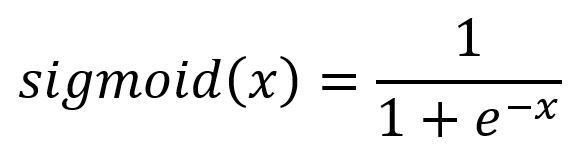
初始权重

权重是用随机值初始化的。假设初始权重如下：

训练样本

考虑如下的三组训练样本，其中上标表示样本的顺序：

• 输入：$x^{(1)}=(2\mathrm{, }3\mathrm{, }1)$, $x^{(2)}=(1\mathrm{, }0\mathrm{, }2)$, $x^{(3)}=(3\mathrm{, }1\mathrm{, }1)$
• 输出：$t^{(1)}=0.64$, $t^{(2)}=0.52$, $t^{(3)}=0.36$

模型训练的首要目标是调整模型的参数（权重），使得在给定输入（$x$）时，预测或计算出的输出（$y$）尽可能接近实际或期望的输出（$t$）。

前向传播过程

输入层 → 隐藏层

神经元 $h_1$ 和 $h_2$ 的计算公式如下：

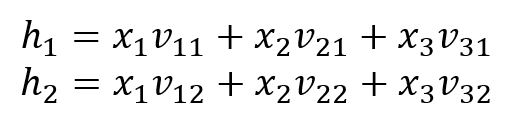
隐藏层 → 输出层

输出值 $y$ 的计算公式如下：

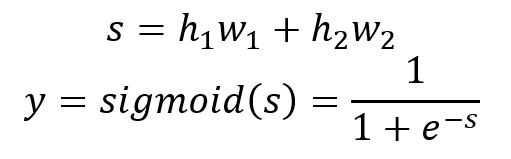
分别对三个样本进行计算：

显然，这三个计算出的输出值（$y$）与期望值（$t$）非常不同。

反向传播过程

损失函数

损失函数（Loss Function）的作用是量化模型输出值与期望值之间的误差。它也被称为目标函数（Objective Function）或成本函数（Cost Function）。这里我们使用均方误差（MSE, Mean-Square Error）作为损失函数 $E$：

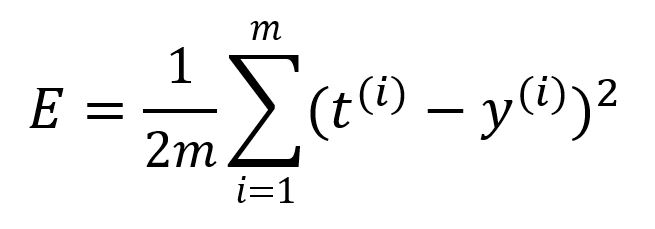
其中 $m$ 为样本数量。计算本轮前向传播的误差为：

损失函数的值越小，意味着模型的准确性越高。模型训练的基本目标就是尽可能减小这个损失函数的值。

将输入和输出视为常数，将模型权重视为损失函数的变量。我们的目标就是调整权重的值，使得损失函数达到最小值——这就是梯度下降技术发挥作用的地方。

在这个示例中，我们将使用批量梯度下降（BGD, Batch Gradient descent），即所有样本都参与梯度的计算。将学习率设定为 $\eta =0.5$。

输出层 → 隐藏层

分别调整权重 $w_1$ 和 $w_2$。

使用链式法则计算 $E$ 相对于 $w_1$ 的偏导数：

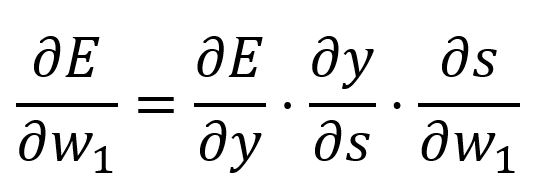
其中，

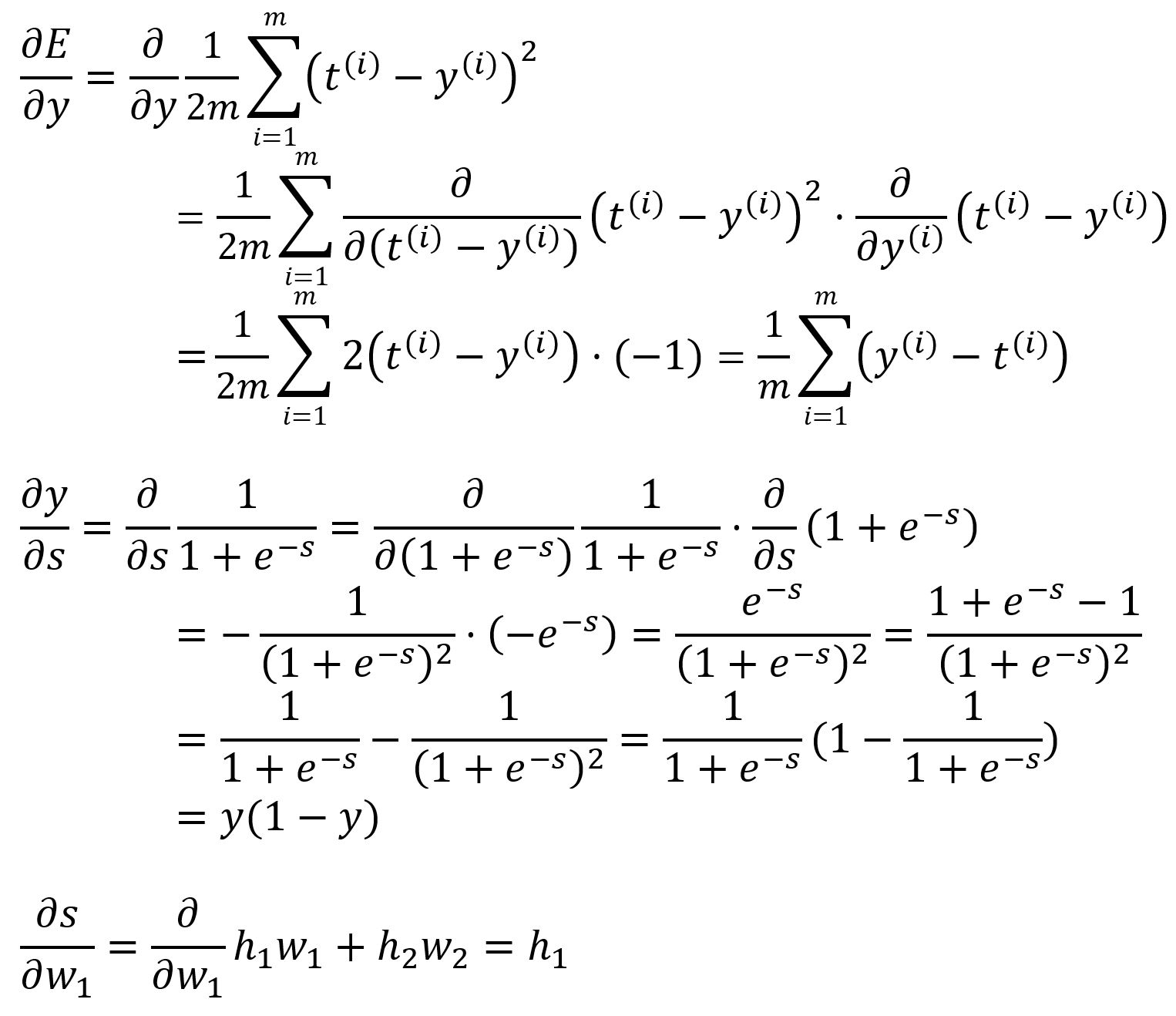
带入数值计算：

于是 $\frac{\partial E}{\partial w_1}=0.294\times 0.152\times 1.5=0.067$

由于所有样本都参与偏导数的计算，在计算 $\frac{\partial y}{\partial s}$ 和 $\frac{\partial s}{\partial w_1}$ 时，我们将这些导数在所有样本上求和，然后取平均值。

因此，$w_1$ 更新为 $w_1=w_1-\eta \frac{\partial E}{\partial w_1}=0.8-0.5\times 0.067=0.766$。

权重 $w_2$ 可以通过计算 $E$ 相对于 $w_2$ 的偏导数来进行类似的调整。在这一轮中，$w_2$ 从 $0.2$ 更新为 $0.167$。

隐藏层 → 输入层

分别调整权重 $v_{11}$ ~ $v_{32}$。

使用链式法则计算 $E$ 相对于 $v_{11}$ 的偏导数：

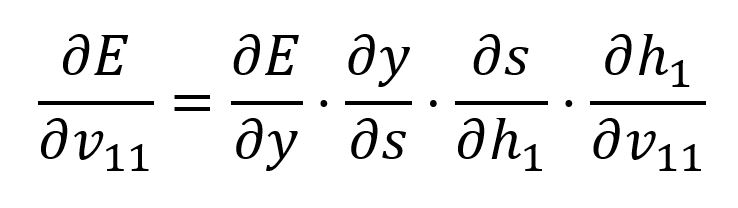
我们已经推导过 $\frac{\partial E}{\partial y}$ 和 $\frac{\partial y}{\partial s}$，后面两个的推导如下：

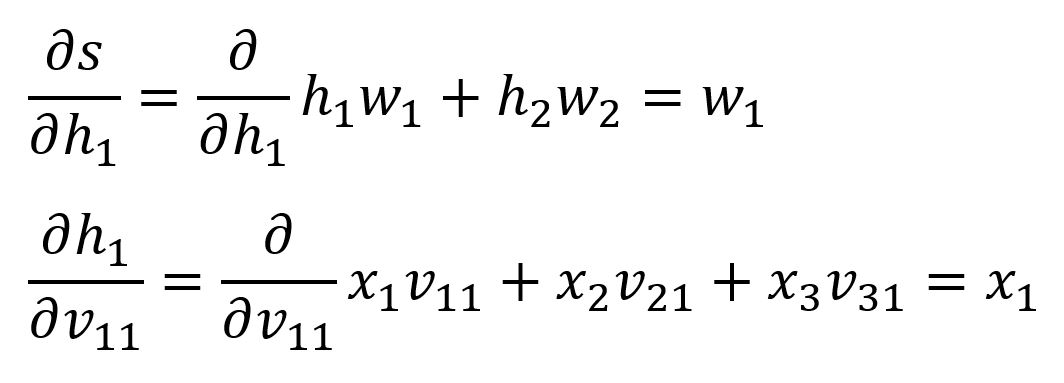
带入数值计算：

于是 $\frac{\partial E}{\partial v_{11}}=0.294\times 0.152\times 0.8\times 2=0.072$。

因此，$v_{11}$ 更新为 $v_{11}=v_{11}-\eta \frac{\partial E}{\partial v_{11}}=0.15-0.5\times 0.072=0.114$。

其余的权重可以通过计算 $E$ 相对于每一个权重的偏导数来进行类似的调整。在这一轮中，它们更新如下：

• $v_{12}$ 从 $0.2$ 更新为 $0.191$
• $v_{21}$ 从 $0.6$ 更新为 $0.576$
• $v_{22}$ 从 $0.3$ 更新为 $0.294$
• $v_{31}$ 从 $0.3$ 更新为 $0.282$
• $v_{32}$ 从 $0.5$ 更新为 $0.496$

迭代训练

将调整后的权重应用到模型中，并继续使用相同的三个样本进行前向传播。在这一迭代中，得到的误差 $E$ 降低为 $0.192$。

反向传播算法迭代执行前向传播和反向传播步骤来训练模型。这个过程会持续直至达到指定的训练次数或时间限制，或者误差降到预定的阈值。