概述
快速随机投影(Fast Random Projection,FastRP)是一种可扩展且高性能的算法,用于学习图中节点的嵌入表示。FastRP实现了节点嵌入的迭代计算,主要包含两个步骤:一是构造节点相似度矩阵构造,二是通过随机投影对矩阵进行降维。
FastRP算法是由H. Chen等人于2019年提出的:
- H. Chen, S.F. Sultan, Y. Tian, M. Chen, S. Skiena, Fast and Accurate Network Embeddings via Very Sparse Random Projection (2019)
FastRP工作框架
FastRP的作者提出,大多数图(节点)嵌入方法基本上由两部分组成:(1)构造一个节点相似度矩阵或从中隐式地采样节点对,然后(2)对该矩阵进行降维得到嵌入结果。
关于降维,许多流行的算法(如Node2Vec)都依赖于Skip-gram等耗时的方法。但作者认为,这些算法的成功并不归功于它们采用的降维方法,而是源于对相似度矩阵的正确构建。
因此,FastRP采用非常稀疏的随机投影(Very Sparse Random Projection)这种可扩展的高效降维技术。
非常稀疏的随机投影
随机投影(Random Projection)是一种降维方法,能够将数据点从高维空间嵌入到低维空间,同时大致保持数据点之间的相对的距离。随机投影的理论基础主要是约翰逊-林登斯特劳斯引理。
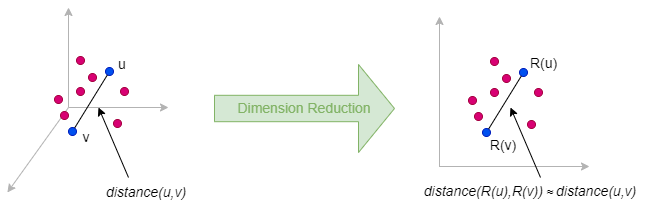
随机投影背后的思想非常简单:要将矩阵Mn×m(对于图数据,有n = m)降维成矩阵Nn×d(d ≪ n),可以简单地将M乘以一个随机投影矩阵Rm×d,即N = M ⋅ R。
矩阵R中的每个元素是独立基于一个分布生成的。具体来说,FastRP采用非常稀疏的随机投影方法,其中R的元素基于以下分布生成:

其中s=sqrt(m)。
非常稀疏的随机投影具有优越的计算效率,因为它只需要进行矩阵乘法,并且R中占比(1-1/s)的元素都为零。
此外,嬴图支持使用一些数值类点属性(特征)来影响矩阵R的初始化。在这种情况下,矩阵R中的每一行由两部分拼接而成:

- 元素d1 ~ dx由非常稀疏随机投影算法生成。
- 元素p1 ~ py是所选节点属性值的线性组合。
- x + y等于最终嵌入的维度,其中y称为属性维度。
- 所选节点属性的数量不必与属性维度相同。
构造节点相似性矩阵
FastRP算法在构建节点相似性矩阵时兼顾以下两点:
- 保留图的高阶接近性
- 对矩阵元素进行归一化处理
令S为图G = (V, E)的邻接矩阵,D为节点度矩阵,A为转移概率矩阵且A = D-1S。下面展示了一个例子,图中每条边上的数字代表边的权重:

事实上,矩阵A中的元素Aij表示从节点i经过长度为1的随机游走到达节点j的概率。进一步地,如果将矩阵A与自身相乘k次得到矩阵Ak,Akij则表示从节点i经过长度为k的随机游走到达节点j的概率。如此,矩阵Ak保留了图的高阶接近性。
但是,当k → ∞,可以证明的是Akij → dj/2m,其中m = |E|,dj是第j个节点的度。由于许多真实世界的图是无标度的,因此Ak中的元素常呈现重尾分布。这意味着Ak中数据点之间的距离主要受具有异常大值的列影响,这使得它们的意义降低,并为下一步降维带来了挑战。
为了解决这个问题,FastRP进一步对矩阵Ak进行归一化处理,方法是将其乘以对角线归一化矩阵L,其中Lij = (dj/2m)β,β是归一化强度。归一化强度控制节点度对嵌入的影响:当β为负时,削弱高节点度邻居的重要性,β为正数时,则相反。
算法步骤
FastRP算法的步骤如下:
- 生成随机映射矩阵R
- 对归一化的1步转移矩阵进行降维:N1 = A ⋅ L ⋅ R
- 对归一化的2步转移矩阵进行降维:N2 = A ⋅ (A ⋅ L ⋅ R) = A ⋅ N1
- 重复步骤3直到对归一化的k步转移矩阵进行降维:Nk = A ⋅ Nk-1
- 生成矩阵A的不同幂次的加权组合结果:N = α1N1 + ... + αkNk,其中α1,...,αk为迭代权重
特殊说明
- FastRP算法忽略边的方向,按照无向边进行计算。
示例图集
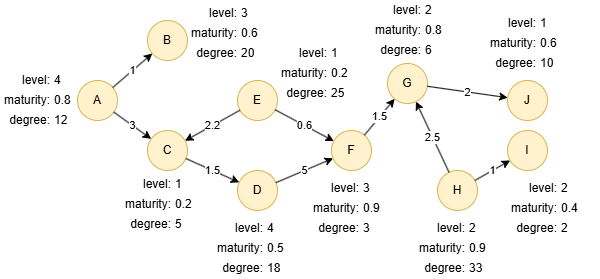
创建示例图集:
// 在空图集中逐行运行以下语句
create().node_property(@default, "level", uint32).node_property(@default, "maturity", float).node_property(@default, "degree", uint32).edge_property(@default, "score", float)
insert().into(@default).nodes([{_id:"A", level:4, maturity:0.8, degree:12},{_id:"B", level:3, maturity:0.6, degree:20},{_id:"C", level:1, maturity:0.2, degree:5},{_id:"D", level:4, maturity:0.5, degree:18},{_id:"E", level:1, maturity:0.2, degree:25},{_id:"F", level:3, maturity:0.9, degree:3},{_id:"G", level:2, maturity:0.8, degree:6},{_id:"H", level:2, maturity:0.9, degree:33},{_id:"I", level:2, maturity:0.4, degree:2},{_id:"J", level:1, maturity:0.6, degree:10}])
insert().into(@default).edges([{_from:"A", _to:"B", score:1}, {_from:"A", _to:"C", score:3}, {_from:"C", _to:"D", score:1.5}, {_from:"D", _to:"F", score:5}, {_from:"E", _to:"C", score:2.2}, {_from:"E", _to:"F", score:0.6}, {_from:"F", _to:"G", score:1.5}, {_from:"G", _to:"J", score:2}, {_from:"H", _to:"G", score:2.5}, {_from:"H", _to:"I", score:1}])
创建HDC图集
将当前图集全部加载到HDC服务器hdc-server-1上,并命名为 hdc_fastRP:
CALL hdc.graph.create("hdc-server-1", "hdc_fastRP", {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static",
query: "query",
default: false
})
hdc.graph.create("hdc_fastRP", {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static",
query: "query",
default: false
}).to("hdc-server-1")
参数
算法名:fastRP
参数名 |
类型 |
规范 |
默认值 |
可选 |
描述 |
|---|---|---|---|---|---|
dimension |
Integer | ≥2 | / | 否 | 嵌入向量的维度 |
normalizationStrength |
Float | / | / | 是 | 归一化强度β |
iterationWeights |
[]Float | ≥0 | [0.0,1.0,1.0] |
是 | 每次迭代的权重,数组长度为迭代轮数 |
edge_schema_property |
[]"@<schema>?.<property>" |
/ | / | 是 | 作为权重的数值类型边属性,权重值为所有指定属性值的总和;不包含指定属性的边将被忽略 |
node_schema_property |
[]"@<schema>?.<property>" |
/ | / | 是 | 作为特征的数值类型点属性;propertyDimension和node_schema_property需同时配置或忽略 |
propertyDimension |
Integer | (0,dimension] |
/ | 是 | 属性维度的长度;propertyDimension和node_schema_property需同时配置或忽略 |
return_id_uuid |
String | uuid, id, both |
uuid |
是 | 在结果中使用_uuid、_id或同时使用两者来表示点 |
limit |
Integer | ≥-1 | -1 |
是 | 限制返回的结果数;-1返回所有结果 |
文件回写
CALL algo.fastRP.write("hdc_fastRP", {
params: {
return_id_uuid: "id",
dimension: 5,
normalizationStrength: 1.5,
iterationWeights: [0, 0.8, 0.2, 1],
edge_schema_property: 'score',
node_schema_property: ['level', 'maturity', 'degree'],
propertyDimension: 2
},
return_params: {
file: {
filename: "embeddings"
}
}
})
algo(fastRP).params({
projection: "hdc_fastRP",
return_id_uuid: "id",
dimension: 5,
normalizationStrength: 1.5,
iterationWeights: [0, 0.8, 0.2, 1],
edge_schema_property: 'score',
node_schema_property: ['level', 'maturity', 'degree'],
propertyDimension: 2
}).write({
file:{
filename: 'embeddings'
}
})
_id,embedding_result
J,-1.12587,-1.20511,-1.12587,0.079247,0.079247,
D,-1.11528,-1.22975,-1.11528,0,0,
F,-1.1547,-1.1547,-1.1547,0,0,
H,-1.07893,-1.15311,-1.22729,0,0,
B,-1.1547,-1.1547,-1.1547,0,0,
A,-1.1547,-1.1547,-1.1547,0,0,
E,-1.12083,-1.12083,-1.21962,0,0,
C,-1.24807,-1.24807,-0.394019,-0.854049,0,
I,-1.1547,-1.1547,-1.1547,0,0,
G,-0.538663,-1.54159,-1.04013,-0.501465,0,
数据库回写
将结果中的embedding_result值写入指定点属性。该属性类型为float[]。
CALL algo.fastRP.write("hdc_fastRP", {
params: {
return_id_uuid: "id",
dimension: 10,
normalizationStrength: 1.5,
iterationWeights: [0, 0.8, 0.2, 1],
edge_schema_property: 'score',
node_schema_property: ['level', 'maturity', 'degree'],
propertyDimension: 2
},
return_params: {
db: {
property: "vector"
}
}
})
algo(fastRP).params({
projection: "hdc_fastRP",
return_id_uuid: "id",
dimension: 10,
normalizationStrength: 1.5,
iterationWeights: [0, 0.8, 0.2, 1],
edge_schema_property: 'score',
node_schema_property: ['level', 'maturity', 'degree'],
propertyDimension: 2
}).write({
db: {
property: "vector"
}
})
完整返回
CALL algo.fastRP("hdc_fastRP", {
params: {
return_id_uuid: "id",
dimension: 3,
normalizationStrength: 1.5,
iterationWeights: [0, 0.8, 0.2, 0.3, 1]
},
return_params: {}
}) YIELD embeddings
RETURN embeddings
exec{
algo(fastRP).params({
return_id_uuid: "id",
dimension: 3,
normalizationStrength: 1.5,
iterationWeights: [0, 0.8, 0.2, 0.3, 1]
}) as embeddings
return embeddings
} on hdc_fastRP
结果:
_id |
embedding_result |
|---|---|
| J | [0.0,2.299999952316284,0.0] |
| D | [0.0,-2.299999952316284,0.0] |
| F | [0.0,0.0,2.299999952316284] |
| H | [-2.299999952316284,0.0,0.0] |
| B | [-2.299999952316284,0.0,0.0] |
| A | [-1.6263456344604492,0.0,-1.6263456344604492] |
| E | [0.0,2.299999952316284,0.0] |
| C | [0.0,0.0,0.0] |
| I | [1.6263456344604492,1.6263456344604492,0.0] |
| G | [0.0,0.0,0.0] |
流式返回
CALL algo.fastRP("hdc_fastRP", {
params: {
return_id_uuid: "id",
dimension: 4,
normalizationStrength: 1.5,
iterationWeights: [0, 0.8, 0.2, 0.3, 1]
},
return_params: {
stream: {}
}
}) YIELD embeddings
RETURN embeddings
exec{
algo(fastRP).params({
return_id_uuid: "id",
dimension: 4,
normalizationStrength: 1.5,
iterationWeights: [0, 0.8, 0.2, 0.3, 1]
}).stream() as embeddings
return embeddings
} on hdc_fastRP
结果:
_id |
embedding_result |
|---|---|
| J | [0.0,-1.6263456344604492,0.0,-1.6263456344604492] |
| D | [1.6263456344604492,0.0,0.0,1.6263456344604492] |
| F | [0.0,0.0,-2.299999952316284,0.0] |
| H | [1.6263456344604492,0.0,0.0,-1.6263456344604492] |
| B | [0.0,-2.299999952316284,0.0,0.0] |
| A | [-1.6263456344604492,-1.6263456344604492,0.0,0.0] |
| E | [0.0,0.0,0.0,-2.299999952316284] |
| C | [0.0,1.6263456344604492,0.0,1.6263456344604492] |
| I | [0.0,0.0,0.0,0.0] |
| G | [-1.3279056549072266,0.0,-1.3279056549072266,1.3279056549072266] |
