概述
CELF(Cost Effective Lazy Forward,具有成本效益的惰性前向选择)算法可以在一个有传播(污染物、信息、病毒等)行为的网络中选取一些种子节点作为传播源头,以达到影响力最大化(Influence Maximization, IM)的效果。
CELF算法由Jure Leskovec等人于2007年提出,它改进了传统基于IC模型的贪心(Greedy)算法,利用函数次模性,只在初始时计算所有节点的影响力,之后不再重复计算所有节点的影响力,因此具有更高的成本效益。
算法的相关资料如下:
- J. Leskovec, A. Krause, C. Guestrin, C. Faloutsos, J. VanBriesen, N. Glance, Cost-effective Outbreak Detection in Networks (2007)
- D. Kempe, J. Kleinberg, E. Tardos, Maximizing the Spread of Influence through a Social Network (2003)
CELF算法的一个典型应用场景是预防流行病爆发,通过选择一小组人进行监测,从而达到在疾病爆发的早期就能发现的效果。
基本概念
传播函数—IC模型
本算法采用独立级联(Independent Cascade, IC)模型来模拟网络中的影响传播过程。IC模型是一种概率型传播模型,它从一批初始被激活的种子节点集合开始,在第k轮:
- 只有在第
k-1轮被激活的节点在第k轮具备激活能力,它们以一定的概率各自尝试激活每个尚未被激活的出边邻居节点。 - 当图中剩余具备激活能力的节点数为0时,传播过程结束。
传播结束时,图中被激活的节点总数就可以衡量种子集合的影响力。为了排除模拟结果的随机性,我们模拟大量次数,然后对所有结果取平均值,这种方法称为蒙特卡罗模拟(Monte-Carlo Simulation)。
次模性
传播函数IC()具有次模性(Submodular,又称子模性),这是指对于一个节点v,它的边际效益(Marginal Gain)随着种子集合S的增大而递减:
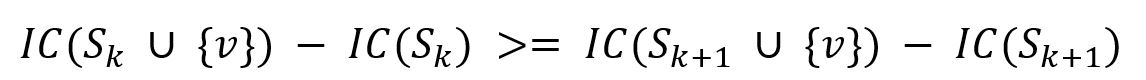
其中种子集合|Sk+1|>|Sk|,S∪{v}表示将节点v加入种子集合。
CELF算法正是利用了传播函数的次模性对传统的贪心算法进行了改进,省去了大量的重复计算从而算地更快,但结果仍接近最优。
惰性前向选择
CELF算法在初始时与贪心算法一样,要计算每个节点的影响力,然后根据影响力大小进行降序排列。由于此时种子集合为空,每个节点的影响力可以被视为各自的初始边际效益。
在第一轮迭代中,将列表最顶部的节点移至种子集合。
下一轮迭代中,只重新计算最顶部节点的边际效益。排序后,如果该节点仍位于最顶部,就可将其移至种子集合;如果不是,重新计算最顶部节点的边际效益并进行排序。
与贪心算法不同,在每轮迭代中,CELF不计算所有剩余节点的边际效益,这就是在利用传播函数的次模性——所有节点在本轮的边际效益只会比上一轮小。因此,如果计算的节点仍处于最顶部,就可以直接将其放入种子集合,无需计算其他节点。
当种子集合达到规定大小时,算法停止。
示例图
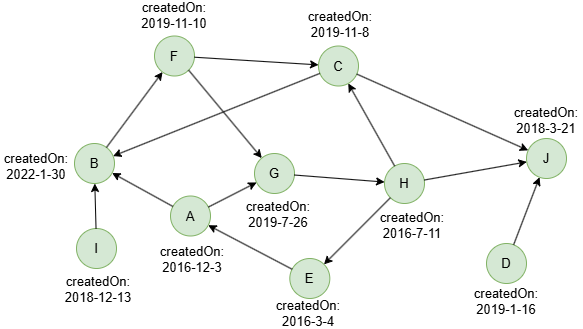
在一个空图中运行以下语句定义图结构并插入数据:
ALTER GRAPH CURRENT_GRAPH ADD NODE {
account ({createdOn datetime})
};
ALTER GRAPH CURRENT_GRAPH ADD EDGE {
follow ()-[]->()
};
INSERT (A:account {_id:"A", createdOn: "2016-12-3"}),
(B:account {_id:"B", createdOn:"2022-1-30"}),
(C:account {_id:"C", createdOn: "2019-11-8"}),
(D:account {_id:"D", createdOn: "2019-1-16"}),
(E:account {_id:"E", createdOn: "2016-3-4"}),
(F:account {_id:"F", createdOn: "2019-11-10"}),
(G:account {_id:"G", createdOn: "2019-7-26"}),
(H:account {_id:"H", createdOn: "2016-7-11"}),
(I:account {_id:"I", createdOn: "2018-12-13"}),
(J:account {_id:"J", createdOn: "2018-3-21"}),
(A)-[:follow]->(B),
(A)-[:follow]->(G),
(B)-[:follow]->(F),
(C)-[:follow]->(B),
(C)-[:follow]->(J),
(D)-[:follow]->(J),
(E)-[:follow]->(A),
(F)-[:follow]->(C),
(F)-[:follow]->(G),
(G)-[:follow]->(H),
(H)-[:follow]->(C),
(H)-[:follow]->(E),
(H)-[:follow]->(J),
(I)-[:follow]->(B);
create().node_schema("account").edge_schema("follow");
create().node_property(@account, "createdOn", datetime);
insert().into(@account).nodes([{_id:"A", createdOn: "2016-12-3"}, {_id:"B", createdOn:"2022-1-30" }, {_id:"C", createdOn: "2019-11-8"}, {_id:"D", createdOn: "2019-1-16"}, {_id:"E", createdOn: "2016-3-4"}, {_id:"F", createdOn: "2019-11-10"}, {_id:"G", createdOn: "2019-7-26"}, {_id:"H", createdOn: "2016-7-11"}, {_id:"I", createdOn: "2018-12-13"},{_id:"J", createdOn: "2018-3-21"}]);
insert().into(@follow).edges([{_from:"A", _to:"B"}, {_from:"A", _to:"G"}, {_from:"B", _to:"F"}, {_from:"C", _to:"J"}, {_from:"D", _to:"J"}, {_from:"E", _to:"A"}, {_from:"F", _to:"C"}, {_from:"F", _to:"G"}, {_from:"G", _to:"H"}, {_from:"H", _to:"C"}, {_from:"H", _to:"E"}, {_from:"H", _to:"J"}, {_from:"I", _to:"B"}, {_from:"C", _to:"B"}]);
创建HDC图
将当前图集全部加载到HDC服务器hdc-server-1上,并命名为 my_hdc_graph:
CREATE HDC GRAPH my_hdc_graph ON "hdc-server-1" OPTIONS {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}
hdc.graph.create("my_hdc_graph", {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}).to("hdc-server-1")
参数
算法名:celf
参数名 |
类型 |
规范 |
默认值 |
可选 |
描述 |
|---|---|---|---|---|---|
seedSetSize |
Integer | >0 | 1 |
是 | 种子节点总数 |
monteCarloSimulations |
Integer | >0 | 1000 |
是 | 蒙特卡罗模拟次数 |
propagationProbability |
Float | (0,1) | 0.1 |
是 | 在指定轮次里,具有激活能力的节点成功激活每个出向邻居的概率 |
return_id_uuid |
String | uuid, id, both |
uuid |
是 | 在结果中使用_uuid、_id或同时使用两者来表示点 |
文件回写
CALL algo.celf.write("my_hdc_graph", {
return_id_uuid: "id",
seedSetSize: 3,
monteCarloSimulations: 1000,
propagationProbability: 0.5
}, {
file: {
filename: "seeds"
}
})
algo(celf).params({
projection: "my_hdc_graph",
return_id_uuid: "id",
seedSetSize: 3,
monteCarloSimulations: 1000,
propagationProbability: 0.5
}).write({
file: {
filename: "seeds"
}
})
结果:
_id,spread
H,3.612
I,1.673
A,1.353
完整返回
CALL algo.celf.run("my_hdc_graph", {
return_id_uuid: "id",
seedSetSize: 2,
monteCarloSimulations: 1000,
propagationProbability: 0.6
}) YIELD seeds
RETURN seeds
exec{
algo(celf).params({
return_id_uuid: "id",
seedSetSize: 2,
monteCarloSimulations: 1000,
propagationProbability: 0.6
}) as seeds
return seeds
} on my_hdc_graph
结果:
| _id | spread |
|---|---|
| H | 4.466 |
| I | 1.714 |
流式返回
CALL algo.celf.stream("my_hdc_graph", {
return_id_uuid: "id",
seedSetSize: 3,
monteCarloSimulations: 1000,
propagationProbability: 0.6
}) YIELD seeds
MATCH (nodes WHERE nodes._id = seeds._id)
RETURN nodes._id, nodes.createdOn, seeds.spread
exec{
algo(celf).params({
return_id_uuid: "id",
seedSetSize: 3,
monteCarloSimulations: 1000,
propagationProbability: 0.6
}).stream() as seeds
find().nodes({_id == seeds._id}) as nodes
return nodes._id, nodes.createdOn, seeds.spread
} on my_hdc_graph
结果:
| nodes._id | nodes.createdOn | seeds.spread |
|---|---|---|
| H | 2016-07-11 00:00:00 | 4.466 |
| I | 2018-12-13 00:00:00 | 1.714 |
| A | 2016-12-03 00:00:00 | 1.168 |
