概述
调和中心性(Harmonic Centrality)是接近中心性的变种。调和中心性提出的平均最短距离能够处理非连通图中会出现的无限值。调和中心性算法首先是由M. Marchiori和V. Latora于2000年提出的,然后由A. Dekker和Y. Rochat分别于2005年和2009年提出:
- M. Marchiori, V. Latora, Harmony in the Small-World (2000)
- A. Dekker, Conceptual Distance in Social Network Analysis (2005)
- Y. Rochat, Closeness Centrality Extended to Unconnected Graphs: The Harmonic Centrality Index (2009)
调和中心性的取值范围是0到1,节点的分值越大,距离其他节点越近。
基本概念
最短距离
两个点之间的最短距离是指它们之间最短路径的边数。具体可参看接近中心性。
调和平均数
调和平均数(Harmonic Mean)是平均数的一种,它是变量倒数的算术平均数的倒数。算数平均数A和调和平均数H的计算公式如下:
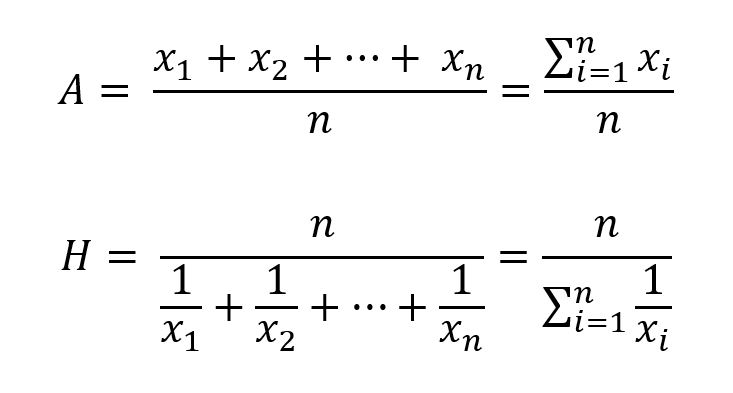
调和平均数应用的经典场景是以不同的速度通过相同的距离时,求平均速度。假设有一个往返行程,去程速度为30 km/h,回程速度为10 km/h,整个行程的平均速度是多少?
这种情况下,直接使用算数平均数A = (30+10)/2 = 20 km/h计算不太合理。由于去程行驶时间少,回程行驶时间多,整个行程大部分时间的速度是10 km/h,因而平均速度应该更接近于10 km/h 才对。
假设单程距离为1,考虑行驶时间而计算的平均值为2/(1/30+1/10) = 15 km/h,这就是调和平均数,它根据每段距离所花费的时间进行了调整。
调和中心性
在本算法中,节点的调和中心性分值等于该点与其他各节点的最短距离调和平均值的倒数。计算公式为:
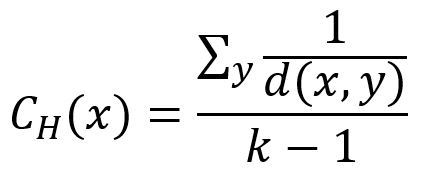
其中,x为待计算的目标节点,y为图中除 x以外的所有节点,k-1为y的个数,d(x,y)为x到y的最短距离,当x与y不连通时,d(i,j) = +∞,则有1/d(i,j) = 0。
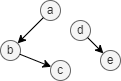
上图中点a的调和中心性为(1 + 1/2 + 1/+∞ + 1/+∞) / 4 = 0.375,点d的调和中心性为(1/+∞ + 1/+∞ + 1/+∞ + 1) / 4 = 0.25。
调和中心性算法会消耗很多计算资源。在一个有V个节点的图中,建议当V>10000 时通过采样进行近似计算,推荐的采样个数是节点数以10为底的对数(
log(V))。
每次执行算法时,只进行一次采样,每个节点的中心性分值是基于该节点到所有样本节点的最短距离计算的。
特殊说明
- 孤点的调和中心性分值为0。
示例图
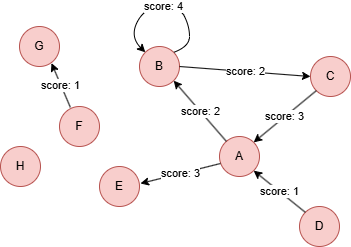
在一个空图中运行以下语句定义图结构并插入数据:
ALTER GRAPH CURRENT_GRAPH ADD NODE {
user ()
};
ALTER GRAPH CURRENT_GRAPH ADD EDGE {
vote ()-[{score uint32}]->()
};
INSERT (A:user {_id: "A"}),
(B:user {_id: "B"}),
(C:user {_id: "C"}),
(D:user {_id: "D"}),
(E:user {_id: "E"}),
(F:user {_id: "F"}),
(G:user {_id: "G"}),
(H:user {_id: "H"}),
(A)-[:vote {score: 2}]->(B),
(A)-[:vote {score: 3}]->(E),
(B)-[:vote {score: 4}]->(B),
(B)-[:vote {score: 2}]->(C),
(C)-[:vote {score: 3}]->(A),
(D)-[:vote {score: 1}]->(A),
(F)-[:vote {score: 1}]->(G);
create().node_schema("user").edge_schema("vote");
create().edge_property(@vote, "score", uint32);
insert().into(@user).nodes([{_id:"A"},{_id:"B"},{_id:"C"},{_id:"D"},{_id:"E"},{_id:"F"},{_id:"G"},{_id:"H"}]);
insert().into(@vote).edges([{_from:"A", _to:"B", score:2}, {_from:"A", _to:"E", score:3}, {_from:"B", _to:"B", score:4}, {_from:"B", _to:"C", score:2}, {_from:"C", _to:"A", score:3}, {_from:"D", _to:"A", score:1}, {_from:"F", _to:"G", score:1}]);
创建HDC图
将当前图集全部加载到HDC服务器hdc-server-1上,并命名为 my_hdc_graph:
CREATE HDC GRAPH my_hdc_graph ON "hdc-server-1" OPTIONS {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}
hdc.graph.create("my_hdc_graph", {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}).to("hdc-server-1")
参数
算法名:harmonic_centrality
参数名 |
类型 |
规范 |
默认值 |
可选 |
描述 |
|---|---|---|---|---|---|
ids |
[]_id |
/ | / | 是 | 通过_id指定参与计算的点;若未设置则计算所有点 |
uuids |
[]_uuid |
/ | / | 是 | 通过_uuid指定参与计算的点;若未设置则计算所有点 |
direction |
String | in, out |
/ | 是 | 指定最短路径中所有边的方向,in表示仅包含入边,out表示仅包含出边 |
edge_schema_property |
[]"<@schema.?><property>" |
/ | / | 是 | 作为权重的数值类型边属性,权重值为所有指定属性值的总和;不包含指定属性的边将被忽略 |
impl_type |
String | dijkstra, delta_stepping, spfa, beta |
beta |
是 | 指定计算加权最短路径的算法:Dijkstra、Delta-Stepping、SPFA或嬴图默认最短路径算法beta。仅当使用edge_schema_property时生效 |
sample_size |
Integer | -1, -2, [1, |V|] |
-2 |
是 | 指定采样策略:
|
return_id_uuid |
String | uuid, id, both |
uuid |
是 | 在结果中使用_uuid、_id或同时使用两者来表示点 |
limit |
Integer | ≥-1 | -1 |
是 | 限制返回的结果数;-1返回所有结果 |
order |
String | asc, desc |
/ | 是 | 根据harmonic_centrality分值对结果排序 |
文件回写
CALL algo.harmonic_centrality.write("my_hdc_graph", {
return_id_uuid: "id",
order: "desc"
}, {
file: {
filename: "harmonic"
}
})
algo(harmonic_centrality).params({
projection: "my_hdc_graph",
return_id_uuid: "id",
order: "desc"
}).write({
file: {
filename: "harmonic"
}
})
结果:
_id,harmonic_centrality
A,0.571429
B,0.428571
C,0.428571
D,0.357143
E,0.357143
F,0.142857
G,0.142857
H,0
数据库回写
将结果中的harmonic_centrality值写入指定点属性。该属性类型为float。
CALL algo.harmonic_centrality.write("my_hdc_graph", {},
{
db: {
property: "hc"
}
})
algo(harmonic_centrality).params({
projection: "my_hdc_graph"
}).write({
db:{
property: 'hc'
}
})
完整返回
CALL algo.harmonic_centrality.run("my_hdc_graph", {
return_id_uuid: "id",
ids: ["A", "B"],
edge_schema_property: "score"
}) YIELD hc
RETURN hc
exec{
algo(harmonic_centrality).params({
return_id_uuid: "id",
ids: ["A", "B"],
edge_schema_property: "score"
}) as hc
return hc
} on my_hdc_graph
结果:
| _id | harmonic_centrality |
|---|---|
| A | 0.309523 |
| B | 0.219048 |
流式返回
CALL algo.harmonic_centrality.stream("my_hdc_graph", {
direction: "in",
return_id_uuid: "id"
}) YIELD hc
FILTER hc.harmonic_centrality = 0
RETURN hc
exec{
algo(harmonic_centrality).params({
direction: "in",
return_id_uuid: "id"
}).stream() as hc
where hc.harmonic_centrality == 0
return hc
} on my_hdc_graph
结果:
| _id | harmonic_centrality |
|---|---|
| D | 0 |
| F | 0 |
| H | 0 |
