概述
最小生成树(Minimum Spanning Tree, MST)算法计算图中每个连通分量的边权重之和最小的生成树。
MST在网络设计、聚类和优化等问题中具有各种应用,其中最小化总成本或权重是重要的目标。
基本概念
生成树
一个生成树(Spanning Tree)是一个连通图G = (V, E)(或一个连通分量)的连通子图,它包含图中的所有节点,并形成一个树结构(即无环)。一个图可能存在多个生成树,而每个生成树必定有(|V| - 1)条边。
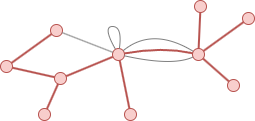
下图中的11个节点和10条用红色突出显示的边构成该图的一个生成树:
最小生成树(MST)
最小生成树(MST)是边权重和最小的生成树。MST的构建从给定的起点开始。起点的选择不会影响MST算法的正确性,但会影响MST的结构和边的添加顺序。不同的起点可能产生不同的MST,但对于给定的图,它们都是有效的MST。
给上面的示例图赋予边权重后,使用不同起点产生的三个可能的MST在下面以红色突出显示:
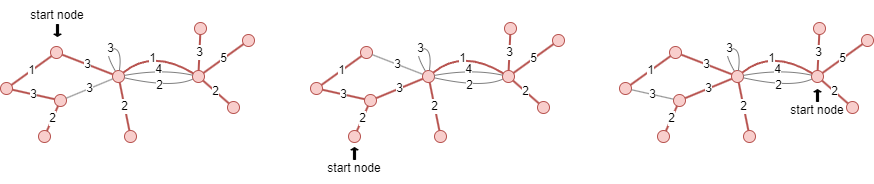
关于起点的选择:
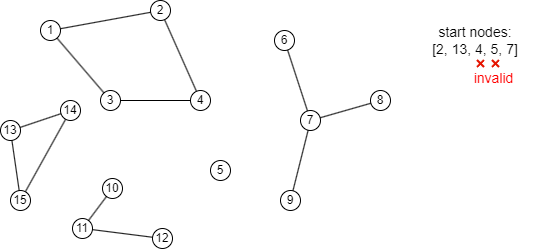
- 每个连通分量只需要一个起点。如果指定了多个起点,只有第一个有效。
- 如果某个连通分量没有指定起点,则不会为其计算MST。
- 孤点不是计算MST的有效起点。
特殊说明
- 最小生成树算法忽略边的方向,按照无向边进行计算。
示例图
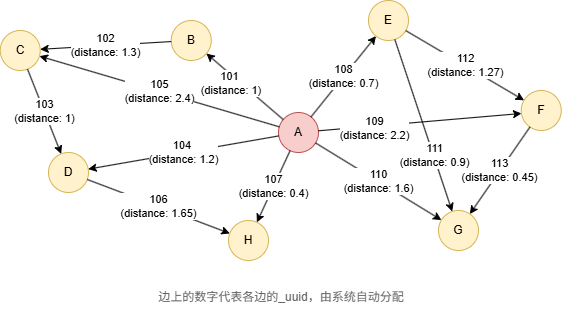
在一个空图中运行以下语句定义图结构并插入数据:
ALTER GRAPH CURRENT_GRAPH ADD NODE {
electricCenter (),
village ()
};
ALTER GRAPH CURRENT_GRAPH ADD EDGE {
connects ()-[{distance float}]->()
};
INSERT (A:electricCenter {_id: "A"}),
(B:village {_id: "B"}),
(C:village {_id: "C"}),
(D:village {_id: "D"}),
(E:village {_id: "E"}),
(F:village {_id: "F"}),
(G:village {_id: "G"}),
(H:village {_id: "H"}),
(A)-[:connects {distance: 1}]->(B),
(A)-[:connects {distance: 2.4}]->(C),
(A)-[:connects {distance: 1.2}]->(D),
(A)-[:connects {distance: 0.7}]->(E),
(A)-[:connects {distance: 2.2}]->(F),
(A)-[:connects {distance: 1.6}]->(G),
(A)-[:connects {distance: 0.4}]->(H),
(B)-[:connects {distance: 1.3}]->(C),
(C)-[:connects {distance: 1}]->(D),
(D)-[:connects {distance: 1.65}]->(H),
(E)-[:connects {distance: 1.27}]->(F),
(E)-[:connects {distance: 0.9}]->(G),
(F)-[:connects {distance: 0.45}]->(G);
create().node_schema("electricCenter").node_schema("village").edge_schema("connects");
create().edge_property(@connects, "distance", float);
insert().into(@electricCenter).nodes([{_id:"A"}]);
insert().into(@village).nodes([{_id:"B"}, {_id:"C"}, {_id:"D"}, {_id:"E"}, {_id:"F"}, {_id:"G"}, {_id:"H"}]);
insert().into(@connects).edges([{_from:"A", _to:"B", distance: 1}, {_from:"B", _to:"C", distance: 1.3},{_from:"C", _to:"D", distance: 1}, {_from:"A", _to:"D", distance: 1.2}, {_from:"A", _to:"C", distance: 2.4}, {_from:"D", _to:"H", distance: 1.65}, {_from:"A", _to:"H", distance: 0.4}, {_from:"A", _to:"E", distance: 0.7}, {_from:"A", _to:"F", distance: 2.2}, {_from:"A", _to:"G", distance: 1.6}, {_from:"E", _to:"G", distance: 0.9}, {_from:"E", _to:"F", distance: 1.27}, {_from:"F", _to:"G", distance: 0.45}]);
创建HDC图
将当前图集全部加载到HDC服务器hdc-server-1上,并命名为 my_hdc_graph:
CREATE HDC GRAPH my_hdc_graph ON "hdc-server-1" OPTIONS {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}
hdc.graph.create("my_hdc_graph", {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}).to("hdc-server-1")
参数
算法名:algo(mst)
参数名 |
类型 |
规范 |
默认值 |
可选 |
描述 |
|---|---|---|---|---|---|
ids |
[]_id |
/ | / | 是 | 通过_id为每个连通分量指定起点;若未设置,系统将自动选择起点 |
uuids |
[]_uuid |
/ | / | 是 | 通过_uuid为每个连通分量指定起点;若未设置,系统将自动选择起点 |
edge_schema_property |
[]"<@schema.?><property>" |
/ | / | 否 | 作为权重的数值类型边属性;对于每条边,指定属性的最小值即为其权重;不包含指定属性的边将被忽略 |
return_id_uuid |
String | uuid, id, both |
uuid |
是 | 在结果中使用_uuid、_id或同时使用两者来表示点。仅可使用_uuid表示边。该选项仅在文件回写模式下生效 |
limit |
Integer | ≥-1 | -1 |
是 | 限制返回的结果数;-1返回所有结果 |
文件回写
CALL algo.mst.write("my_hdc_graph", {
return_id_uuid: "id",
ids: ["A"],
edge_schema_property: "distance"
}, {
file: {
filename: "paths"
}
})
algo(mst).params({
projection: "my_hdc_graph",
return_id_uuid: "id",
ids: ["A"],
edge_schema_property: "distance"
}).write({
file: {
filename: "paths"
}
})
结果:
A--[107]--H
A--[108]--E
E--[111]--G
F--[113]--G
A--[101]--B
A--[104]--D
C--[103]--D
完整返回
CALL algo.mst.run("my_hdc_graph", {
ids: ["A"],
edge_schema_property: "@connects.distance"
}) YIELD mst
RETURN mst
exec{
algo(mst).params({
ids: ["A"],
edge_schema_property: "@connects.distance"
}) as mst
return mst
} on my_hdc_graph
结果:
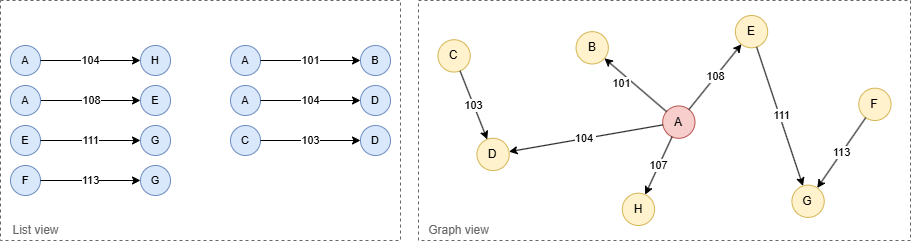
流式返回
CALL algo.mst.stream("my_hdc_graph", {
ids: ["A"],
edge_schema_property: "distance"
}) YIELD mst
FOR e1 IN pedges(mst)
MATCH ()-[e2 WHERE e2._uuid = e1._uuid]->()
RETURN sum(e2.distance)
exec{
algo(mst).params({
ids: ["A"],
edge_schema_property: "distance"
}).stream() as mst
uncollect pedges(mst) as e1
find().edges({_uuid == e1._uuid}) as e2
return sum(e2.distance)
} on my_hdc_graph
结果:5.65
