Skip-gram(SG)模型是自然语言处理(NLP, Natural Language Processing)领域中用于创建词嵌入的重要方法。它也被用于图嵌入算法,如Node2Vec和Struc2Vec,来生成节点嵌入。
背景介绍
Skip-gram模型来源于Word2Vec算法。Word2Vec将单词映射到一个向量空间,在这个向量空间中,语义相似的单词由距离接近的向量表示。Google的T. Mikolov等人于2013年提出Word2Vec。
- T. Mikolov, K. Chen, G. Corrado, J. Dean, Efficient Estimation of Word Representations in Vector Space (2013)
- X. Rong, word2vec Parameter Learning Explained (2016)
在图嵌入领域,一般认为是2014年提出的DeepWalk算法首次将Skip-gram模型应用于生成图中节点的向量表示。其核心概念是将节点视为“单词”,将随机游走生成的节点序列视为“句子”和“语料库”。
- B. Perozzi, R. Al-Rfou, S. Skiena, DeepWalk: Online Learning of Social Representations (2014)
后续提出的Node2Vec、Struc2Vec等图嵌入算法对DeepWalk进行了若干改进,但都仍使用Skip-gram模型。
接下来,我们将使用Skip-gram原始应用的自然语言作为例子进行说明。
模型概览
Skip-gram的基本模式是通过给定的一个目标词(Targat Word)预测出它的若干个上下文单词(Context Word)。如下图所示,单词被输入模型,然后模型生成与相关的四个上下文词汇:、、和。在这里,符号/表示与目标词的前后上下文。生成的上下文单词数量可以根据需要进行调整。
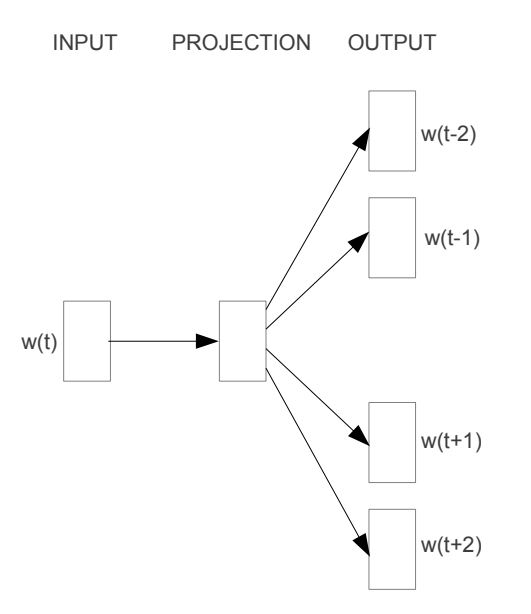
然而,很重要的一点是,Skip-gram模型的最终目标并不是预测。它的真正任务是获得映射关系中的权重矩阵(在图中表示为PROJECTION),该权重矩阵代表了单词的向量表示。
语料库
语料库(Corpus)是模型用来学习单词之间语义关系的句子或文本集合。
假设一个语料库中的所有不同单词组成一个大小为10的词汇表(Vocabulary),这些单词分别是:graph、is、a、good、way、to、visualize、data、very、at。
语料库中包含一系列若干这些单词构成的句子,其中一个是:
Graph is a good way to visualize data.
滑动窗口采样
Skip-gram模型采用滑动窗口采样(Sliding Window Sampling)技术来生成训练样本。这种方法使用一个“窗口”,依次将窗口的中心目标位置放在句子中的每个单词上。目标单词分别与它前后范围在window_size内的每个上下文单词组合在一起。
以下是当window_size时抽样过程的示例:
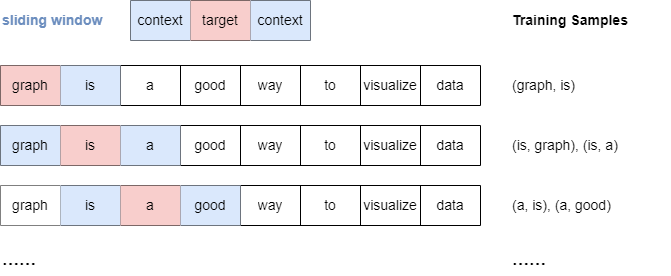
需要留意的是,当window_size时,所有落在窗口内的上下文单词,无论它们与目标单词的距离远近,其重要性没有区别。
独热编码
模型无法直接识别单词,因此必须将单词转换为机器可读的表示形式。
对单词进行编码的一种常见方法是独热编码(One-hot Encoding)。在这种方法中,每个单词被表示为一个唯一的二进制向量,其中只有一个元素是“热”的(),而其他所有元素都是“冷”的()。向量中的位置对应于词汇表中单词的索引。
以下是将独热编码应用于示例词汇表的结果:
| 单词 | 独热编码向量 |
|---|---|
| graph | |
| is | |
| a | |
| good | |
| way | |
| to | |
| visualize | |
| data | |
| very |
模型架构
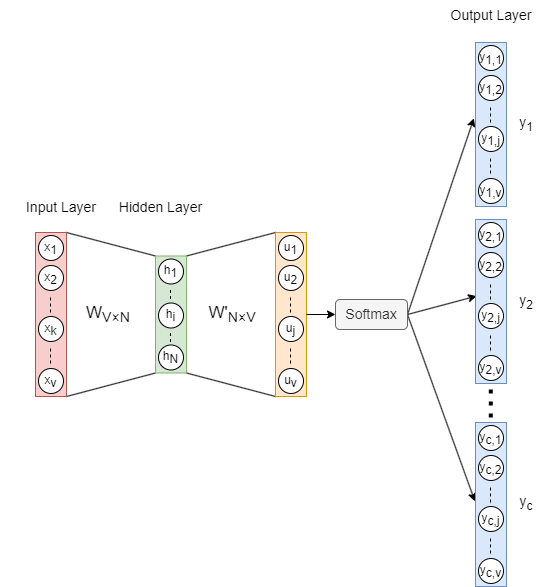
Skip-gram模型的架构如上所示,其中:
- 输入向量是目标单词的独热编码,是词汇表中的单词数。
- 是输入层 → 隐藏层的权重矩阵,是单词嵌入的维度。
- 是隐藏层向量。
- 是隐藏层 → 输出层的权重矩阵。和不同,不是的转置。
- 是应用激活函数Softmax前的向量。
- 每个输出向量()也被称为一个面板(Panel),个面板对应于目标单词的个上下文单词。
Softmax:激活函数Softmax能够将一个数值向量归一化为一个概率分布向量。转换后的向量中,所有分量的概率总和等于。Softmax的公式如下:
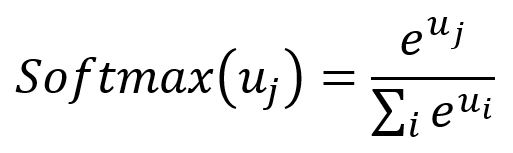
前向传播过程
在我们的示例中, = 10,设置 = 2。先随机初始化权重矩阵和,如下所示。接着,我们将使用样本 (is, graph)、(is, a) 进行说明。
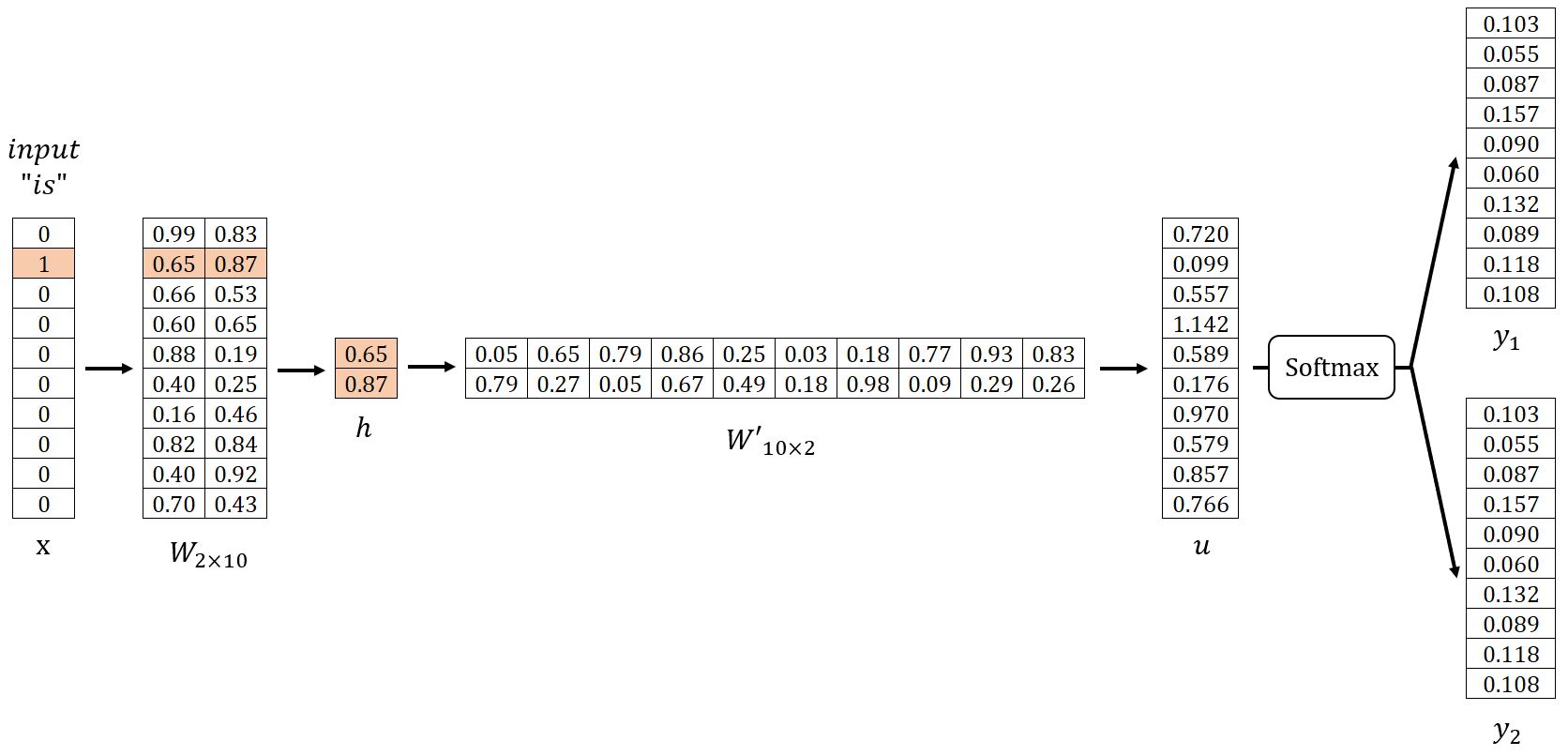
输入层 → 隐藏层
计算隐藏层向量:
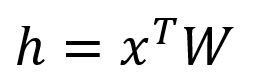
由于是一个仅有的独热编码向量,就对应于矩阵的第行。这个操作本质上是一个简单的查表(Lookup)过程:
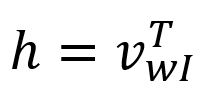
其中是目标单词的输入向量(Input Vector)。
事实上,矩阵的每一行,表示为,将被视为词汇表中每个单词的最终嵌入结果。
隐藏层 → 输出层
计算向量:
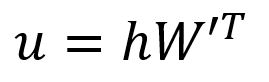
向量的第个分量等于向量与矩阵的第列向量的转置的点积:
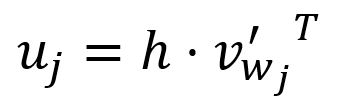
其中,是词汇表中第个单词的输出向量(Output Vector)。
在Skip-gram模型的设计中,词汇表中的每个单词都有两种不同的表示:输入向量和输出向量。输入向量代表单词作为目标词时的表示,而输出向量则代表单词作为上下文词时的表示。
在计算过程中,本质上是目标单词的输入向量与词汇表中第个单词的输出向量的点积。Skip-gram模型的设计原则之一是,两个向量越相似,它们的点积就越大。
此外,值得强调的是,Skip-gram最终只使用输入向量作为单词的嵌入表示。输入和输出向量的分离简化了计算过程,并且提高了模型训练的效率和准确性。
计算输出面板:
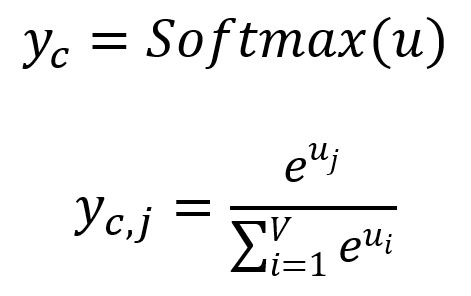
其中,是的第个分量,表示考虑给定目标词时,预测得出词汇表中第个单词的概率。显然,所有概率的总和为。
概率最高的个词被视为预测的上下文词。在我们的示例中,,预测的上下文词分别是good和visualize。

反向传播过程
损失函数
我们希望最大化个真实的上下文单词的概率,即最大化这些概率的乘积:
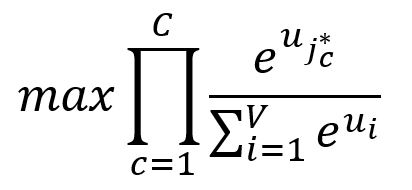
其中,是期望的第个输出上下文单词的索引。
由于在通常情况下,最小化的目标更为直观和易行,因此我们对上述目标进行一些转换:
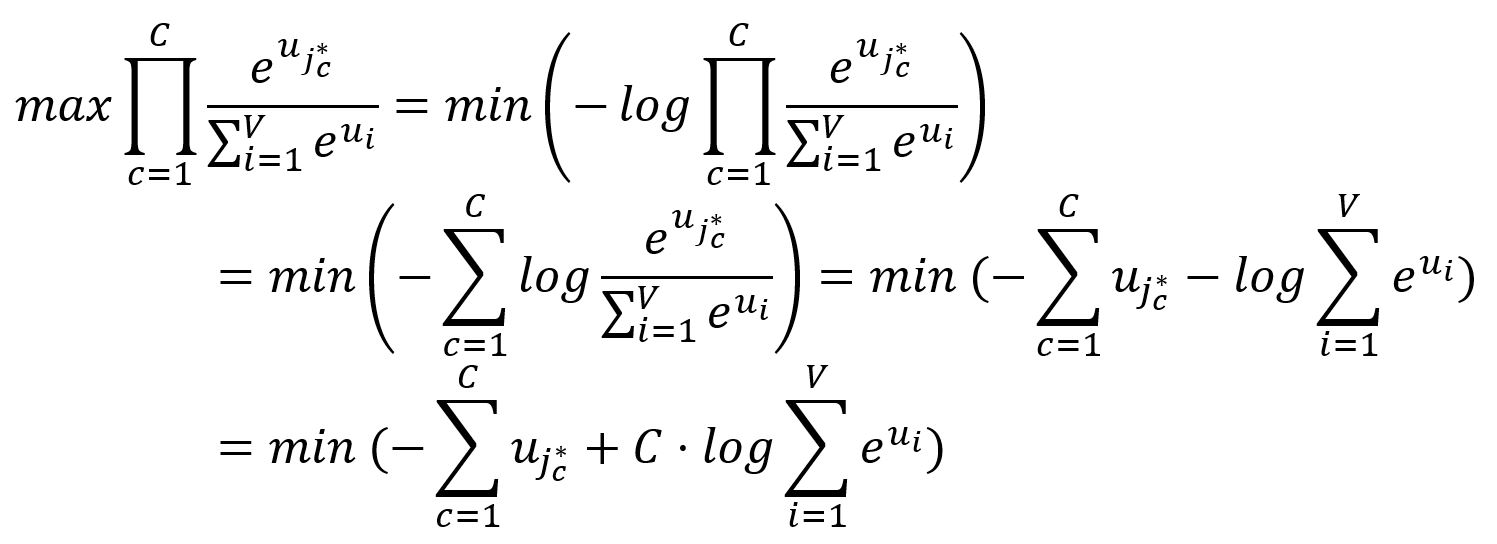
因此,Skip-gram的损失函数为:
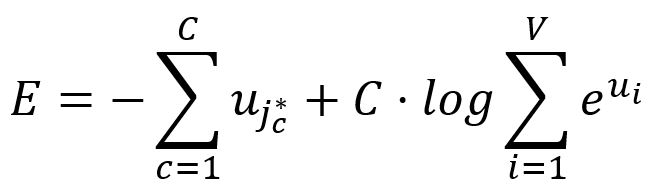
计算相对于的偏导数:
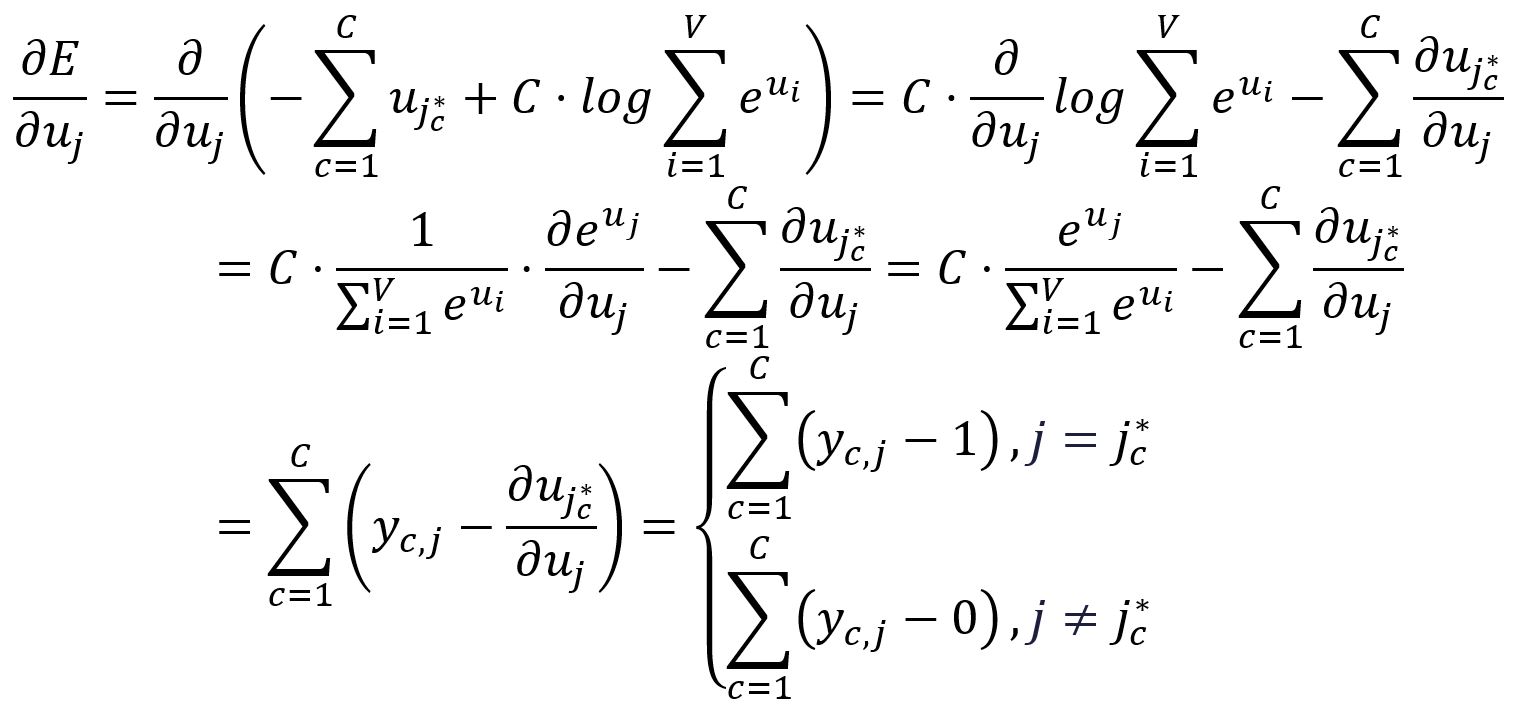
为了简化后续的表示,定义以下内容:
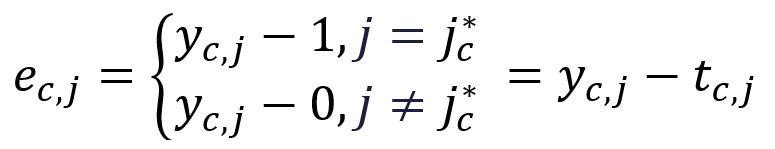
其中,是第个期望输出上下文单词的独热编码向量。在我们的示例中,和是单词graph和a的独热编码向量,因此计算得到和如下:
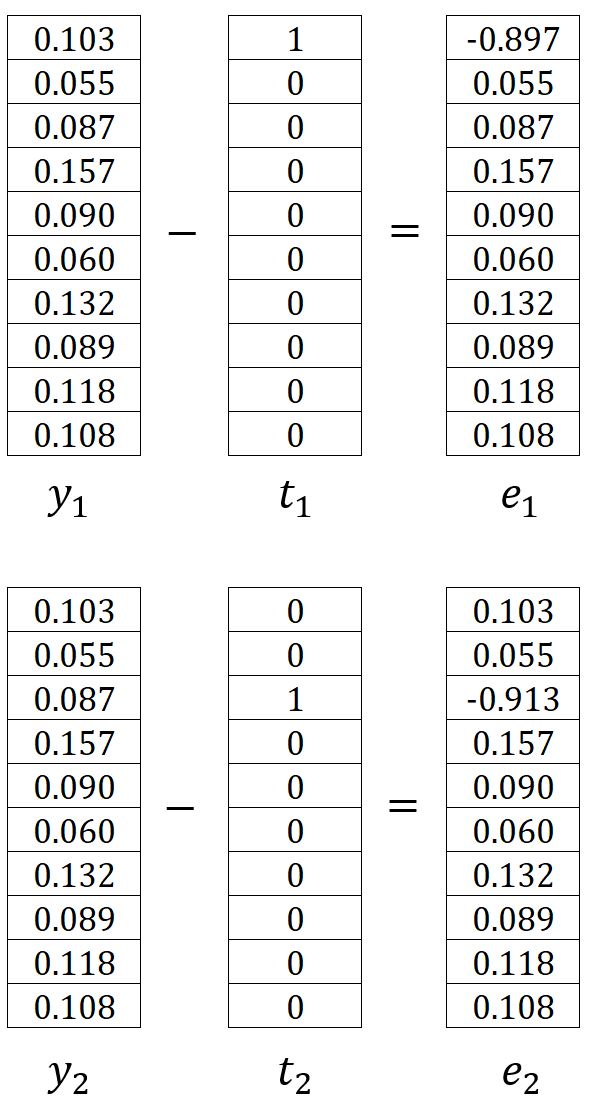
因此,可以写成:
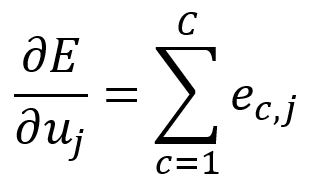
带入示例中的数值进行计算:
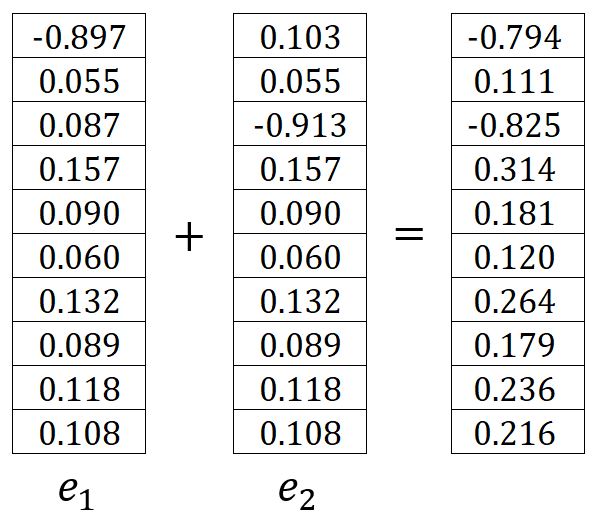
输出层 → 隐藏层
调整矩阵中的所有权重,这意味着所有单词的输出向量都会更新。
计算相对于的偏导数:
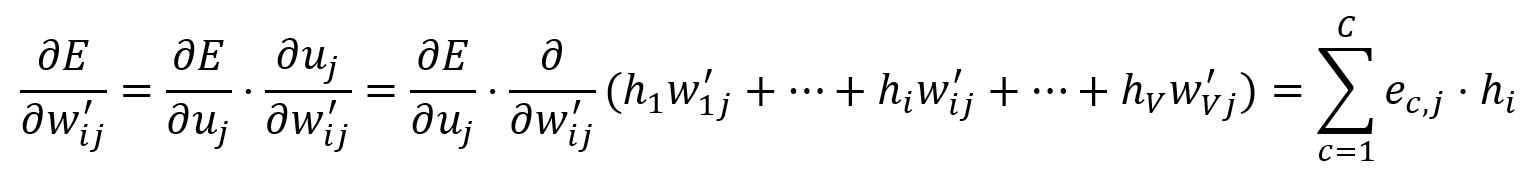
根据学习率调整:
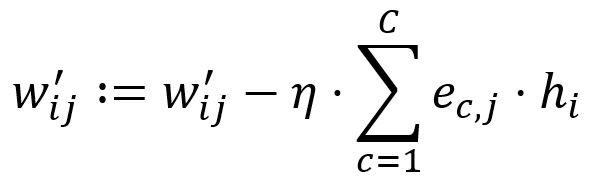
设置。举例来说,和被更新为:
隐藏层 → 输入层
只调整矩阵中与目标单词输入向量相对应的权重。
向量是通过查找矩阵的第行获得的(假设):
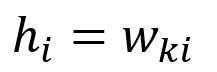
计算相对于的偏导数:
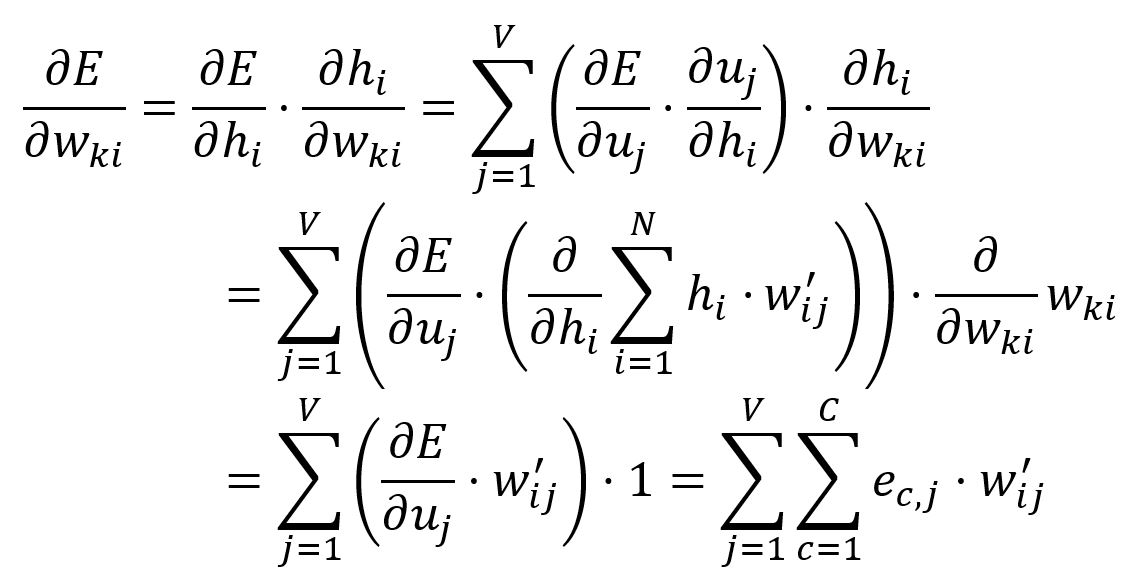
根据学习率调整:
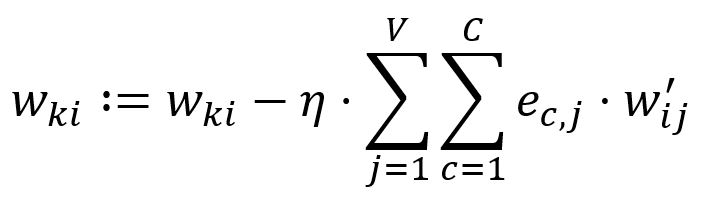
在我们的示例中,等于
优化计算效率
我们已经探讨了Skip-gram模型的原始形式。然而,为了确保模型在实际应用中的计算复杂性保持可行和实用,必须加入一些优化措施。点击这里继续阅读。
