概述
三角形计算(Triangle Counting)算法能识别图中的三角形,三角形表示一组相互连接的三个节点。三角形计算能够体现图中任意三个点之间形成环路的能力。
社交网络中的三角形表示存在有凝聚力的社区,识别三角形有助于理解网络中个人或群体的聚类和相互联系。在金融网络或交易网络中,三角形的存在可能表示存在可疑或欺诈活动,三角形计数可以帮助识别可能需要进一步调查的交易模式。
基本概念
三角形
在复杂图中,任意两点之间可以有多条边,这导致三个节点可能形成超过一个三角形。以下图为例:
- 计算按边组装的不同三角形,有4个。
- 计算按点组装的不同三角形,有2个。

在复杂图中,按边组装的三角形数量往往大于按点组装的三角形数量。组装原则应根据分析目标和应用场景而定。在社交网络分析中,重点通常是理解个体之间的连接模式,因此通常采用按点组装的原则。在金融网络分析或其他类似的领域,重点往往是节点之间的关系,例如金融交易或交互,按边组装原则通常是首选,因为这样可以检查节点连接的紧密程度以及资金或信息如何流经网络。
特殊说明
- 三角形计算算法忽略边的方向,按照无向边进行计算。
示例图
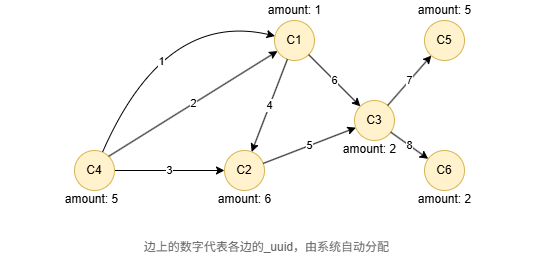
在一个空图中运行以下语句定义图结构并插入数据:
AALTER NODE default ADD PROPERTY {
amount int32
};
INSERT (C1:default {_id: "C1", amount: 1}),
(C2:default {_id: "C2", amount: 6}),
(C3:default {_id: "C3", amount: 2}),
(C4:default {_id: "C4", amount: 5}),
(C5:default {_id: "C5", amount: 5}),
(C6:default {_id: "C6", amount: 2}),
(C4)-[:default]->(C1),
(C4)-[:default]->(C1),
(C4)-[:default]->(C2),
(C1)-[:default]->(C2),
(C2)-[:default]->(C3),
(C1)-[:default]->(C3),
(C3)-[:default]->(C5),
(C3)-[:default]->(C6);
create().node_property(@default, "amount", int32);
insert().into(@default).nodes([{_id:"C1", amount: 1}, {_id:"C2", amount: 6}, {_id:"C3", amount: 2}, {_id:"C4", amount: 5}, {_id:"C5", amount: 5}, {_id:"C6", amount: 2}]);
insert().into(@default).edges([{_from:"C4", _to:"C1"}, {_from:"C4", _to:"C1"}, {_from:"C4", _to:"C2"}, {_from:"C1", _to:"C2"}, {_from:"C2", _to:"C3"}, {_from:"C1", _to:"C3"}, {_from:"C3", _to:"C5"}, {_from:"C3", _to:"C6"}]);
在HDC图上运行算法
创建HDC图
将当前图集全部加载到HDC服务器hdc-server-1上,并命名为 my_hdc_graph:
CREATE HDC GRAPH my_hdc_graph ON "hdc-server-1" OPTIONS {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}
hdc.graph.create("my_hdc_graph", {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}).to("hdc-server-1")
参数
算法名:triangle_counting
参数名 |
类型 |
规范 |
默认值 |
可选 |
描述 |
|---|---|---|---|---|---|
type |
Integer | 1, 2 |
1 |
是 | 设置为1时,按边组装三角形;为2时,按点组装三角形 |
result_type |
Integer | 1, 2 |
1 |
是 | 设置为1时,返回三角形数量;为2时,返回每个三角形中的点或边 |
return_id_uuid |
String | uuid, id, both |
uuid |
是 | 在结果中使用_uuid、_id或同时使用两者来表示点。只能使用_uuid来表示边 |
limit |
Integer | ≥-1 | -1 |
是 | 限制返回的结果数;-1返回所有结果 |
文件回写
CALL algo.triangle_counting.write("my_hdc_graph", {
type: 1,
result_type: 2
}, {
file: {
filename: "byEdges"
}
})
algo(triangle_counting).params({
projection: "my_hdc_graph",
type: 1,
result_type: 2
}).write({
file: {
filename: "byEdges"
}
})
结果:
_edge_uuids
1,3,4
2,3,4
6,5,4
CALL algo.triangle_counting.write("my_hdc_graph", {
return_id_uuid: "id",
type: 2,
result_type: 2
}, {
file: {
filename: "byNodes"
}
})
algo(triangle_counting).params({
projection: "my_hdc_graph",
return_id_uuid: "id",
type: 2,
result_type: 2
}).write({
file: {
filename: "byNodes"
}
})
结果:
_node_ids
C1,C4,C2
C1,C3,C2
统计回写
CALL algo.triangle_counting.write("my_hdc_graph", {}, {
stats: {}
})
algo(triangle_counting).params({
projection: "my_hdc_graph"
}).write({
stats: {}
})
结果:
| triangle_count |
|---|
| 3 |
完整返回
CALL algo.triangle_counting.run("my_hdc_graph", {
result_type: 1
}) YIELD r
RETURN r
exec{
algo(triangle_counting).params({
result_type: 1
}) as r
return r
} on my_hdc_graph
结果:
| triangle_count |
|---|
| 3 |
流式返回
CALL algo.triangle_counting.stream("my_hdc_graph", {
return_id_uuid: "id",
type: 2,
result_type: 2
}) YIELD r
RETURN r
exec{
algo(triangle_counting).params({
return_id_uuid: "id",
type: 2,
result_type: 2
}).stream() as r
return r
} on my_hdc_graph
结果:
| _ids |
|---|
| ["C1","C4","C2"] |
| ["C1","C3","C2"] |
统计返回
CALL algo.triangle_counting.stats("my_hdc_graph", {
result_type: 1
}) YIELD stats
RETURN stats
exec{
algo(triangle_counting).params({
result_type: 1
}).stats() as stats
return stats
} on my_hdc_graph
结果:
| triangle_count |
|---|
| 3 |
在分布式投影上运行算法
创建分布式投影
将图集全部投影到shard服务器上并命名为myProj:
CREATE PROJECTION myProj OPTIONS {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true
}
create().projection("myProj", {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true
})
参数
算法名:triangle_counting
参数名 |
类型 |
规范 |
默认值 |
可选 |
描述 |
|---|---|---|---|---|---|
result_type |
Integer | 1, 2 |
1 |
是 | 设置为1时,返回三角形数量;为2时,返回每个三角形中的点或边 |
limit |
Integer | ≥-1 | -1 |
是 | 限制返回的结果数;-1返回所有结果 |
该算法的分布式版本仅按点组装三角形。
文件回写
CALL algo.triangle_counting.write("myProj", {
result_type: 1
}, {
file: {
filename: "triCnt"
}
})
algo(triangle_counting).params({
projection: "myProj",
result_type: 1
}).write({
file: {
filename: "triCnt"
}
})
triangle
2
CALL algo.triangle_counting.write("myProj", {
result_type: 2
}, {
file: {
filename: "triNodes"
}
})
algo(triangle_counting).params({
projection: "myProj",
result_type: 2
}).write({
file: {
filename: "triNodes"
}
})
triangle
216173881625411585,3386708019294240770,13330655996528295937
216173881625411585,10088064264821538817,13330655996528295937
结果中使用点的
_uuid值。
